Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

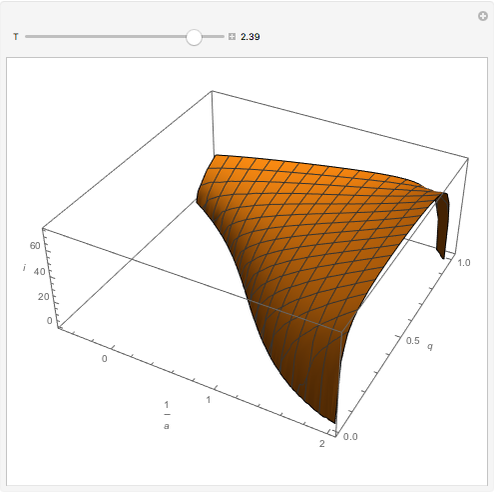
Surfaces of Constant Tisserand Parameter

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

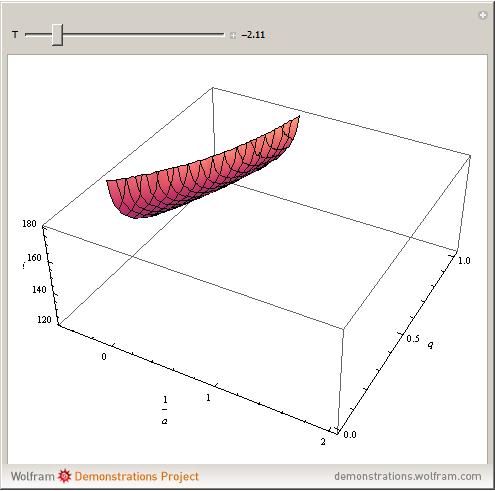
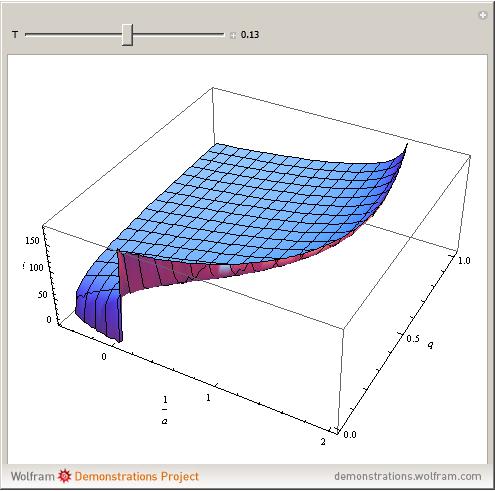
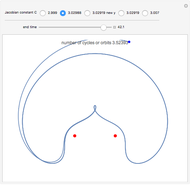
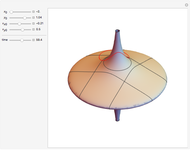
The Tisserand parameter is a constant in the frame of the restricted circular three-body problem (RC3BP) given by , where (the ratio of the semimajor axes of the body and planet), is the eccentricity, and is the inclination of the body's orbit with respect to the planet's orbit.

[more]

This Demonstration plots surfaces of constant Tisserand parameters in the space , where . A body encountering the planet must have , (which means ), and in units of the RC3BP. As the body encounters the planet, its orbital elements change but conserve . The plot shows all possible orbital evolutions for the body for a given value of . The boundary between asteroids and comets in the solar system occurs for .

[less]

Contributed by: Tabaré Gallardo (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

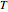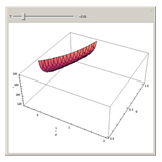
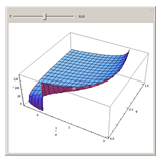
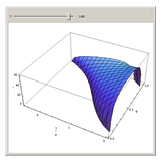
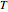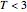It is possible to rearrange in terms of , , and . Given the body's orbital elements, calculate and choose that value in the control; the resulting surface is the possible region in the space which the body can reach after successive encounters with the planet. We assume that the body reaches the planet's orbit and that imposes , , and in units of the RC3BP. See details in Solar System Dynamics.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send