The First 1936 Elegant Binary Turing Machines

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
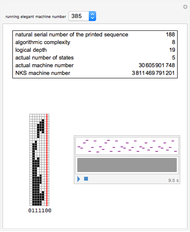
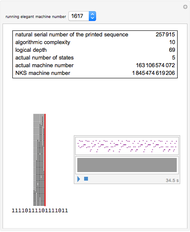
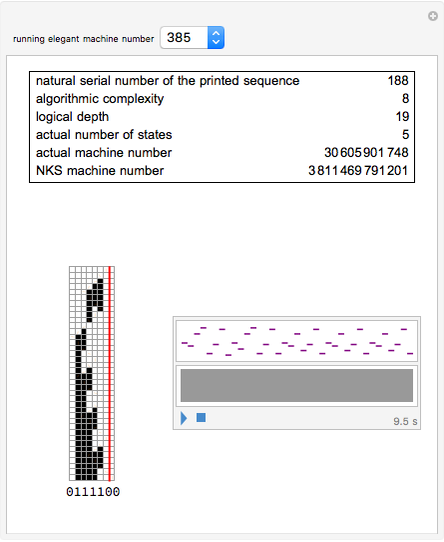
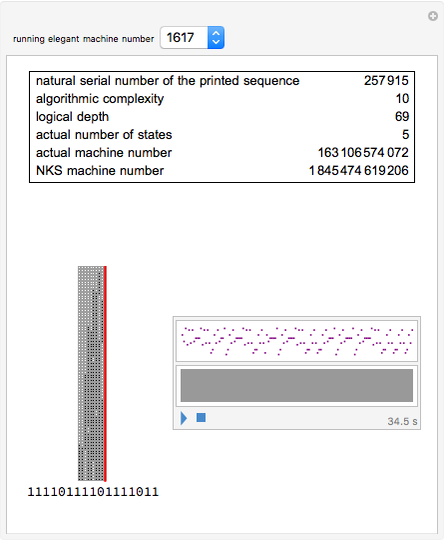
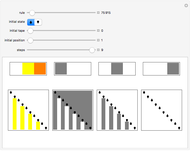
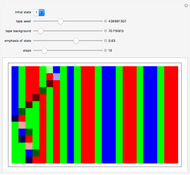
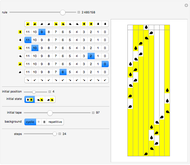
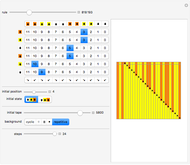
A simple binary Turing machine (SBTM) is said to be elegant if it halts printing a sequence not printed by a machine of lower number. Because of the undecidability of the halting problem, the list of elegant machines is not computable. However, the beginning of that list is computable. We have predetermined (in C++) the first 1936 elegant machines (all 8 two-state, all 31 three-state, all 283 four-state, and only the first 1614 five-state machines). This Demonstration illustrates their evolution with a self-explanatory picture and a sound file.
Contributed by: André Hautot (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The SBTM here have  states (
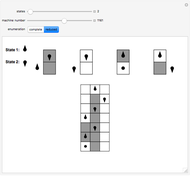
states ( ) and two characters (0 and 1) and they mainly respect the NKS design: a left semi-infinite initially blank tape (full of zeros) and no explicit halting state. The head is initially in state 0 (other states are
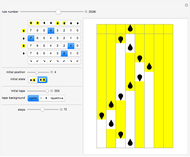
) and two characters (0 and 1) and they mainly respect the NKS design: a left semi-infinite initially blank tape (full of zeros) and no explicit halting state. The head is initially in state 0 (other states are  ), located at the rightmost allowed position. The machine halts when the head tries to enter the forbidden right part of the tape (thus crossing the red line). The sequence printed is read from left to right starting with the greatest position on the left ever attained by the head. Machines are numbered as in NKS with a slight difference. In the instructions table, Table[Doubles->Triples], the doubles are ordered in descending order of both states and characters. The reason is a simplification in theorems like this: "All odd machines halt in one step".
), located at the rightmost allowed position. The machine halts when the head tries to enter the forbidden right part of the tape (thus crossing the red line). The sequence printed is read from left to right starting with the greatest position on the left ever attained by the head. Machines are numbered as in NKS with a slight difference. In the instructions table, Table[Doubles->Triples], the doubles are ordered in descending order of both states and characters. The reason is a simplification in theorems like this: "All odd machines halt in one step".
The sound files were constructed as follows: a machine evolution is completely described by the ordered sequence of the activated triples. Coding each triple by an integer in base  , one gets an evolution sequence translatable as a set of notes in a chromatic scale centered on middle C. The machine evolution then sounds like a chromatic (atonal) melody. Similar sound files exist in the cases of periodic or nested machines (not considered here).
, one gets an evolution sequence translatable as a set of notes in a chromatic scale centered on middle C. The machine evolution then sounds like a chromatic (atonal) melody. Similar sound files exist in the cases of periodic or nested machines (not considered here).
The Snapshots show machines printing sequences of increasing logical depth.
The natural serial number of a sequence follows the enumeration  . SBTM rearrange that list in order of increasing complexity. The process can be viewed as a natural compression method.
. SBTM rearrange that list in order of increasing complexity. The process can be viewed as a natural compression method.
The algorithmic complexity of a sequence is equal to the number of significant binary digits of its elegant machine number.
The logical depth of a sequence is equal to the integer  , where
, where  is the number of steps.
is the number of steps.
A single instruction, ChangeNumbering[n], permutes our numbering with that used in NKS. It works in both directions.
Permanent Citation