Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Time-Averaged Moiré Fringes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

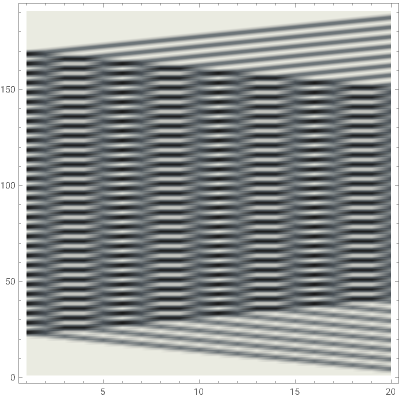
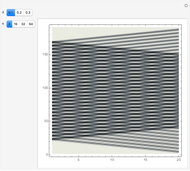
This Demonstration illustrates the formation of time-averaged moiré fringes. The horizontal axis stands for the amplitude of harmonic oscillation ; the vertical axis represents the longitudinal coordinate . Stationary moiré grating is visualized at . Time-averaged images of the moiré grating are shown at increasing amplitudes of oscillation. The parameter controls the density of the moiré grating lines. The parameter controls the number of discrete time nodes in a period of the oscillation used to integrate the dynamical process. Double exposure fringes are produced at ; time-averaged fringes are produced at . One can observe the development of time-averaged fringes at increasing .

Contributed by: Algiment Aleksa and Minvydas Ragulskis (Research Group for Mathematical and Numerical Analysis of Dynamical Systems) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

[1] M. Ragulskis, "Time-Averaged Patterns Produced by Stochastic Moiré Gratings," Computers and Graphics, 33(2), 2009 pp. 147–150.

[2] M. Ragulskis, L. Saunoriene, and R. Maskeliunas, "The Structure of Moiré Grating Lines and Its Influence to Time-Averaged Fringes," Experimental Techniques, 33(2), 2009 p. 60–64.

[3] M. Ragulskis and Z. Navickas, "Time Average Geometric Moiré—Back to the Basics," Experimental Mechanics, 49(4), 2009 pp. 439-450.

[4] M. Ragulskis, A. Aleksa, and R. Maskeliunas, "Contrast Enhancement of Time-Averaged Fringes Based on Moving Average Mapping Functions," Optics and Lasers in Engineering, 47(7-8), 2009 pp. 768–773.

[5] M. Ragulskis and A. Aleksa, "Image Hiding Based on Time-Averaging Moire," Optics Communications, 282(14), 2009 pp. 2752–2759.

http://www.personalas.ktu.lt/~mragul

Permanent Citation

Algiment Aleksa and Minvydas Ragulskis (Research Group for Mathematical and Numerical Analysis of Dynamical Systems) "Time-Averaged Moiré Fringes"
http://demonstrations.wolfram.com/TimeAveragedMoireFringes/
Wolfram Demonstrations Project
Published: March 7 2011

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send