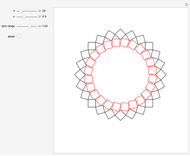
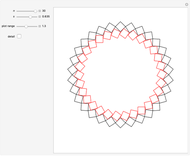
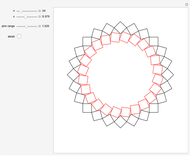
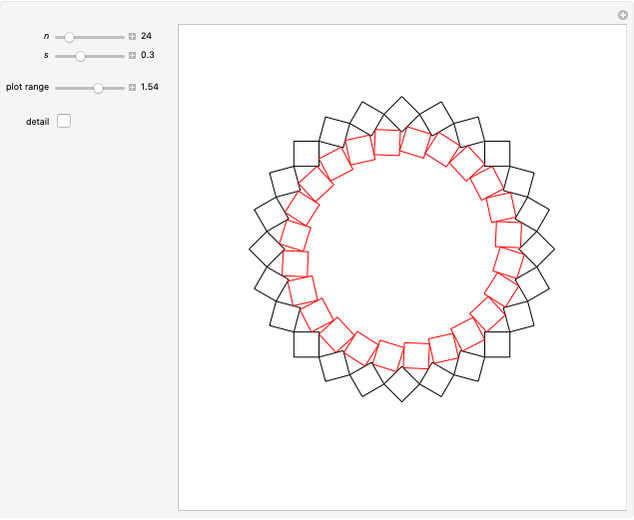
2. Families of Four-Point Touching Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
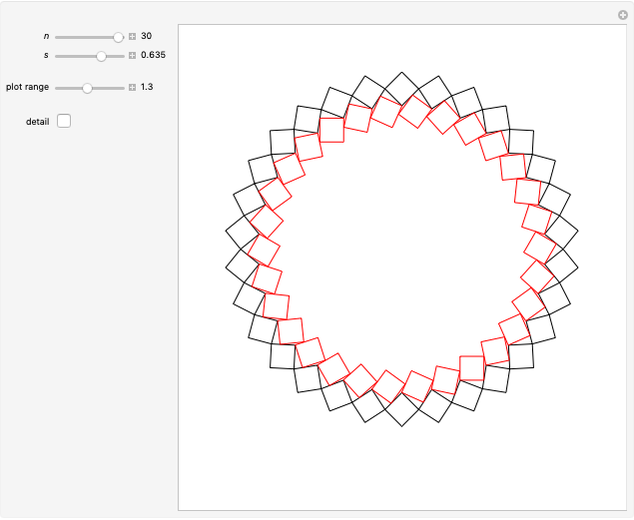
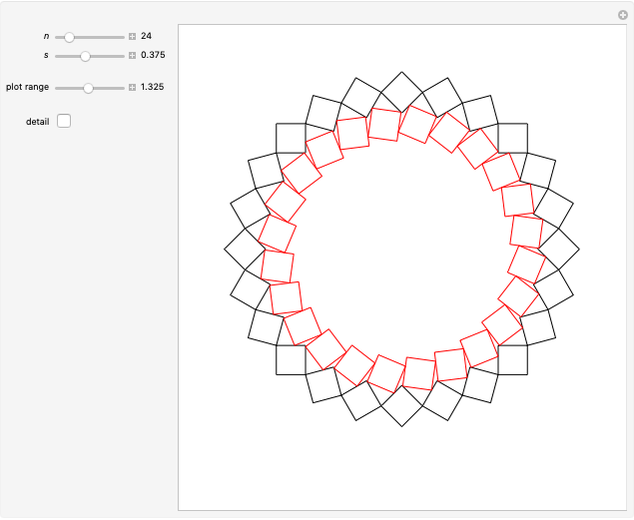
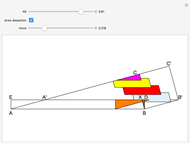
This Demonstration shows four-point touching families of 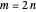 squares, where
squares, where 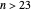 . The parameter
. The parameter  determines the point
determines the point 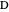 by
by 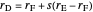 , where
, where 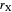 is the radius vector of a point
is the radius vector of a point 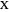 .
. This generalizes [1], where
This generalizes [1], where 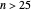 . In this Demonstration you can vary
. In this Demonstration you can vary  within an appropriate range to maintain four-point touching in a family with
within an appropriate range to maintain four-point touching in a family with 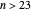 .
.
Contributed by: Izidor Hafner (May 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A family 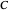 is said to be
is said to be  -touching provided each element of
-touching provided each element of 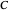 has a nonempty intersection with precisely
has a nonempty intersection with precisely  other elements of
other elements of 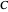 . A
. A  -touching family
-touching family 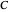 is said to be point-
is said to be point- -touching if any two touching sets have only a single common point [2].
-touching if any two touching sets have only a single common point [2].
Grünbaum has shown that example 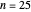 (with dihedral symmetry) in [3] is impossible. He has also said that it is not clear whether there are any point-4-touching families with fewer than 48 squares.
(with dihedral symmetry) in [3] is impossible. He has also said that it is not clear whether there are any point-4-touching families with fewer than 48 squares.
References
[1] I. Hafner. "Families of Four-Point Touching Squares" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/FamiliesOfFourPointTouchingSquares.
[2] B. Grünbaum, "Families of Point-Touching Squares," Geombinatorics, 12(4), 2003 pp. 167–174. (Mar 27, 2019) sites.math.washington.edu/~grunbaum/Familiesofpointtouchin.pdf.
[3] E. Friedman, "Squares Touching a Constant Number of Other Squares," Geombinatorics, 12(2), 2002 pp. 55–60.
Permanent Citation