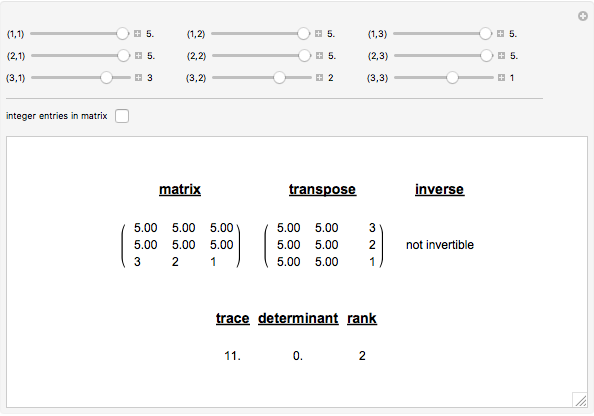
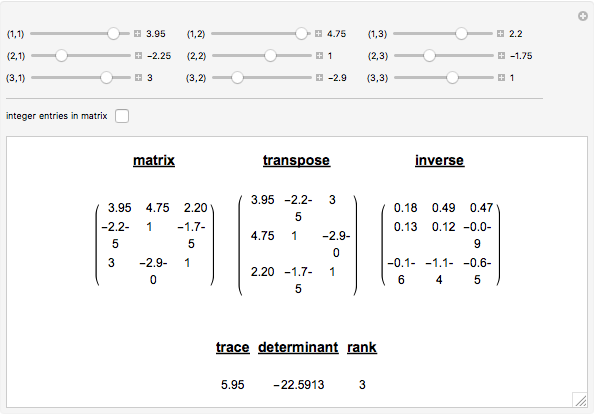
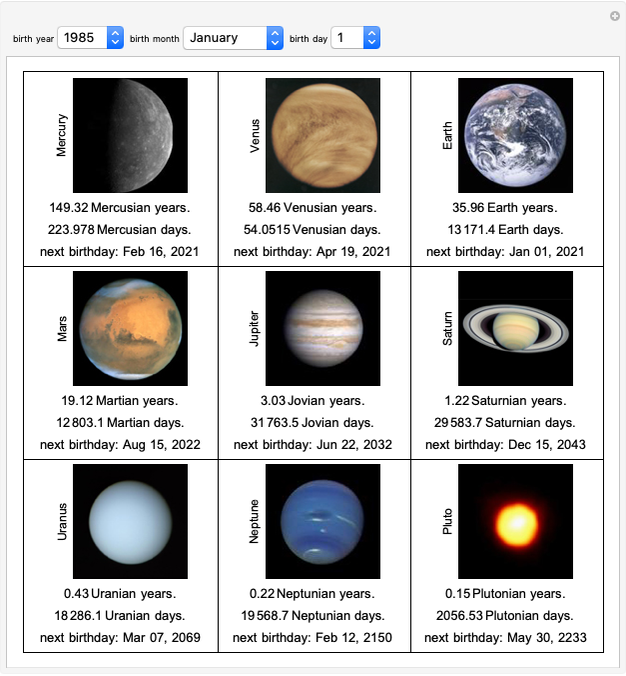
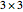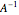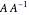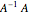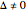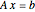3x3 Matrix Transpose, Inverse, Trace, Determinant and Rank
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
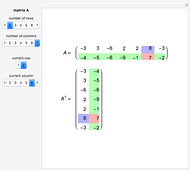
The transpose of a matrix 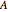 is a matrix
is a matrix 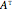 whose rows and columns are reversed.
whose rows and columns are reversed.
Contributed by: Chris Boucher (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation