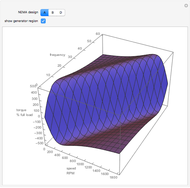
AC Power Factor Principle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
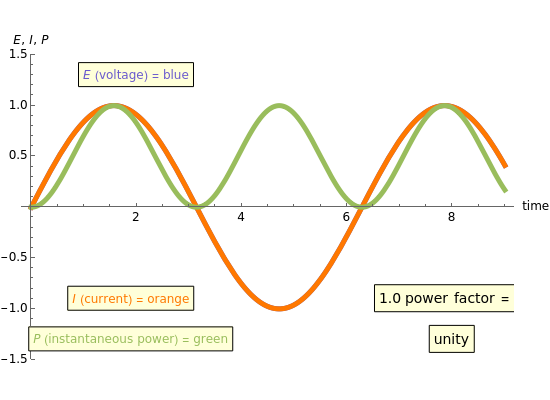
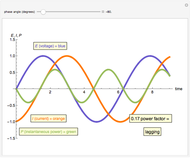
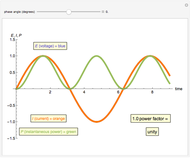
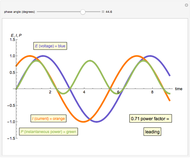
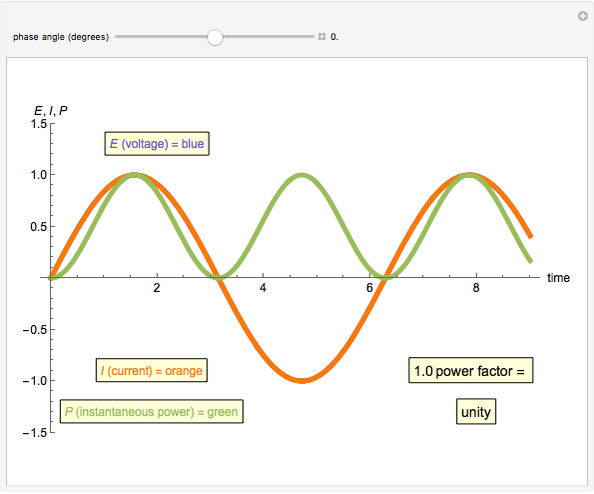
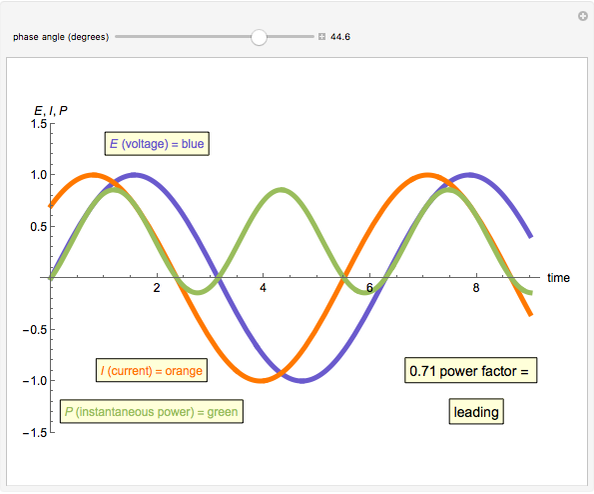
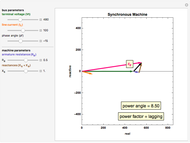
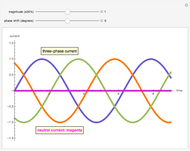
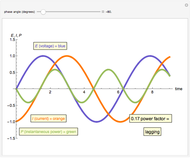
An AC power system power factor is illustrated using a three-trace plot. The phase relationship between voltage and current can reduce the efficiency of power transmission and is known as the power factor. The power trace shows the instantaneous magnitude and direction of the power flow.
Contributed by: Harley H. Hartman (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The power factor PF is mathematically defined as the cosine of the phase angle between voltage and current. True power is defined by the equation 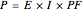 . The graphical representation produces a product of the voltage and current. This product is represented as a sine wave, which is twice the frequency of the voltage and current and represents the instantaneous power and its direction. If the power sine wave is completely on the positive side of the axis, it shows that the power in the system is traveling only in one direction, toward the load. The area under this power sine wave curve represents the amount of energy delivered to the load. If the power sine wave is shifted, the difference in area between the positive and the negative sides represents the power delivered to the load. The negative side of the power sine wave represents the reflected power from a reactive load. A lagging power factor is one in which the current is lagging behind the voltage and is characteristic of an inductive load. A leading power factor is one in which the current is leading the voltage and is characteristic of a capacitive load. If the phase angle were to be shifted to be greater than 90 degrees in either direction, the load would effectively become the source.
. The graphical representation produces a product of the voltage and current. This product is represented as a sine wave, which is twice the frequency of the voltage and current and represents the instantaneous power and its direction. If the power sine wave is completely on the positive side of the axis, it shows that the power in the system is traveling only in one direction, toward the load. The area under this power sine wave curve represents the amount of energy delivered to the load. If the power sine wave is shifted, the difference in area between the positive and the negative sides represents the power delivered to the load. The negative side of the power sine wave represents the reflected power from a reactive load. A lagging power factor is one in which the current is lagging behind the voltage and is characteristic of an inductive load. A leading power factor is one in which the current is leading the voltage and is characteristic of a capacitive load. If the phase angle were to be shifted to be greater than 90 degrees in either direction, the load would effectively become the source.
Permanent Citation
"AC Power Factor Principle"
http://demonstrations.wolfram.com/ACPowerFactorPrinciple/
Wolfram Demonstrations Project
Published: March 7 2011