A'Campo's Link of a Divide

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
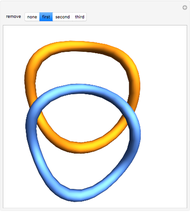
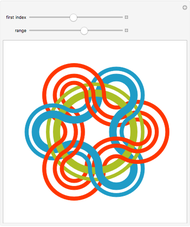
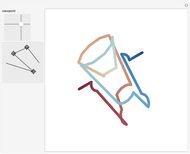
N. A'Campo describes a manner of producing a knot in the 3-sphere from a proper immersion of an arc in the unit disk. Here is a version that uses a polygonal path in a square to form a "long" knot in 3-space. The 2D slider at the top left changes the viewing angle. Move the three locators to change the polygonal path.
Contributed by: Ken Baker (March 2011)
After work by: Norbet A'Campo
Open content licensed under CC BY-NC-SA
Snapshots
Details
N. A'Campo developed a family of knots in the 3-sphere that satisfy many nice properties in the following way:
First view the 3-sphere as a subset of the tangent space over the plane by taking the set of tangent vectors  at a point
at a point  such that
such that 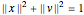 . This restricts
. This restricts  to lie in the unit disk. Given a proper smooth immersion of the closed interval into the unit disk, the tangencies at each point on the curve give two points in the 3-sphere (except at the origin and at the boundary).
to lie in the unit disk. Given a proper smooth immersion of the closed interval into the unit disk, the tangencies at each point on the curve give two points in the 3-sphere (except at the origin and at the boundary).
A'Campo describes this in http://arxiv.org/abs/math/9803081.
See also M. Hirasawa, "Visualization of A'Campo's Fibered Links and Unknotting Operation," Topology and Its Applications, 121(1–2), 2002 pp. 287–304.
One may care to generalize this Demonstration to use more than three points, use smooth curves, interact with the plot of the knot more directly, or just make it run more smoothly.
Permanent Citation
"A'Campo's Link of a Divide"
http://demonstrations.wolfram.com/ACamposLinkOfADivide/
Wolfram Demonstrations Project
Published: March 7 2011