Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

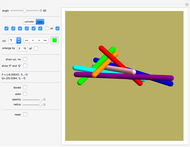
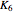Intrinsically Knotted Graphs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

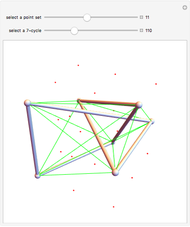
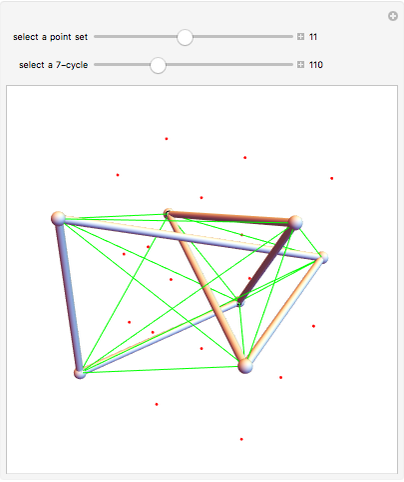
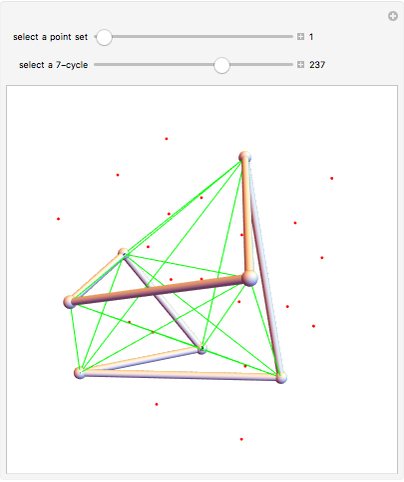
In 1983, Conway and Gordon proved that for every 3D embedding of 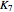(the complete graph on seven points), at least one of the 7-cycles would be knotted. The graph 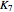is thus called an intrinsically knotted graph.

[more]

Similarly, the graph is intrinsically linked, because it will always contain two linked 3-cycles.

[less]

Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The 23 given point embeddings have the property that no set of four points is on a plane.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send