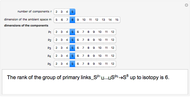
The Ranks of the Groups of Links
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
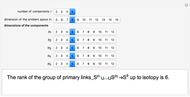
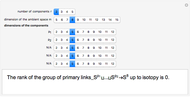
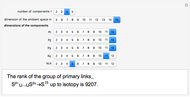
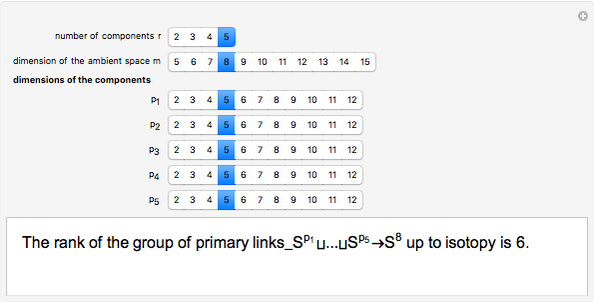
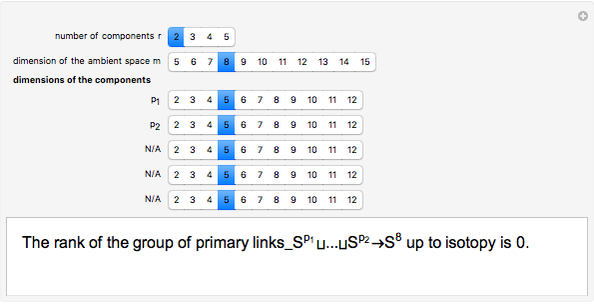
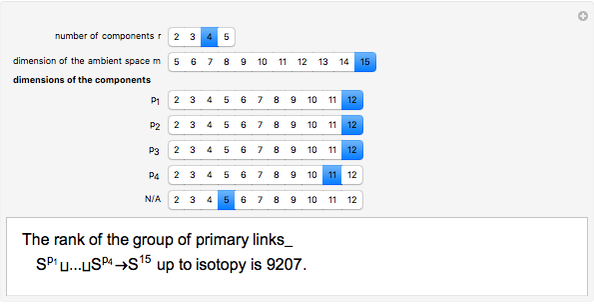
The group of links in codimension greater than two is the group of isotopy classes of smooth embeddings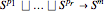 
, where 
are positive integers. A link is primary, if it becomes trivial after removing any of its components. This application computes the rank of the group of primary links of given dimensions 
.
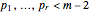Contributed by: Mikhail Skopenkov (May 2011)
(Institute for Information Transmission Problems of the Russian Academy of Sciences, and King Abdullah University of Science and Technology)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This application is based on the formula given in [1].
References
[1] D. Crowley, S. C. Ferry, and M. Skopenkov, "The Rational Classification of Links of Codimension > 2." (May 2011) http://www.math.rutgers.edu/~sferry/ps/RCL24-MS.pdf.
[2] A. Haefliger, "Differentiable Links," Topology, 1, 1962 pp. 241–244.
[3] V. Nezhinsky, "Some Computations in Higher Dimensional Link Theory," Siberian Mathematical Journal, 24(4), 1982 pp. 104–115 (in Russian).
Permanent Citation
"The Ranks of the Groups of Links"
http://demonstrations.wolfram.com/TheRanksOfTheGroupsOfLinks/
Wolfram Demonstrations Project
Published: May 23 2011
Linked Torus Knots
Michael Schreiber
A'Campo's Link of a Divide
Ken Baker
Borromean Ring Removal
Michael Schreiber
Creating and Manipulating Knots
Karl Scherer
The Alexander Polynomial of a Knot
Maxim Rytin
Paradoxical Triangular Braid
Tom Verhoeff
Parity Entangled Links
Michael Schreiber
Lie Subgroups of the 2D Torus Group
Rod Vance (a.k.a. The Wet Savanna Animal)
Intrinsically Knotted Graphs
Ed Pegg Jr
Surfaces Defined on Torus Knots
Enrique Zeleny
