A Double Parabola with Retroreflection Properties

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
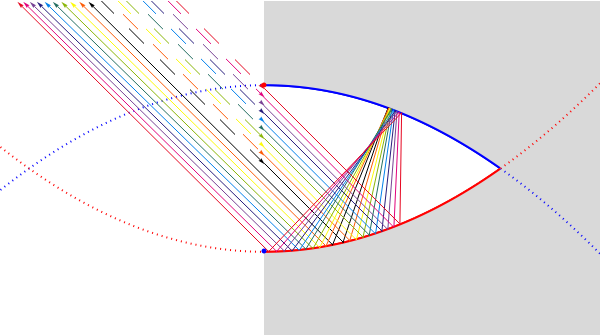
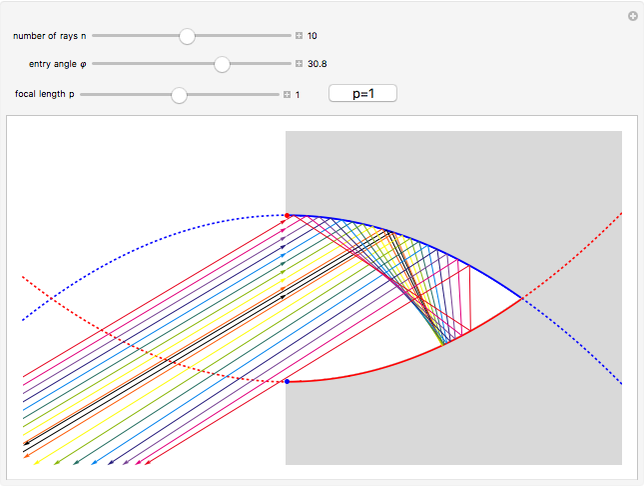
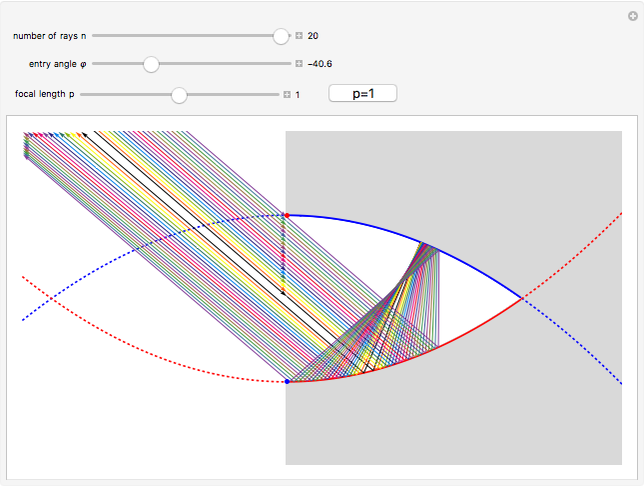
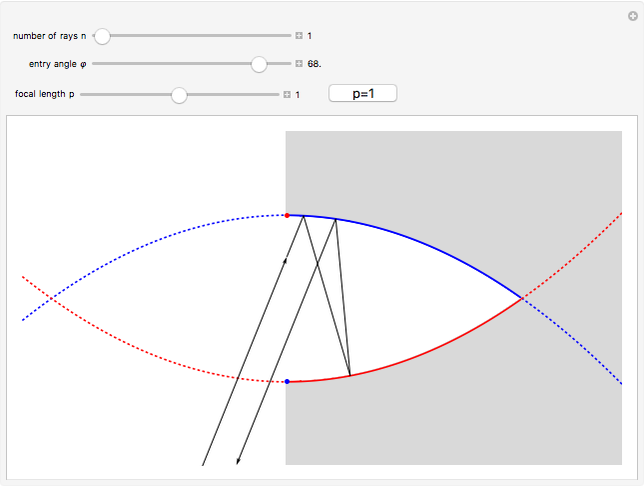
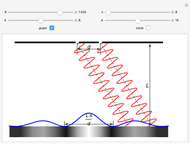
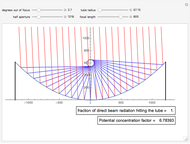
This Demonstration shows the reflective behavior of a two-dimensional shape formed by similar arcs of two parabolas. An interesting and unexpected reflective behavior arises when this shape takes a specific configuration, with two parabolas of unit focal length. In this particular configuration it is found that, except for the rays with absolute value of the entry angle  less than
less than 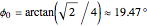 , a ray emerges from the cavity with a trajectory that is nearly opposite to its entry trajectory. This characterizes a cavity with retroreflective behavior. Even in the case of trajectories with entry angle
, a ray emerges from the cavity with a trajectory that is nearly opposite to its entry trajectory. This characterizes a cavity with retroreflective behavior. Even in the case of trajectories with entry angle  below
below  (shown as dashed trajectories), the exit direction does not appear to vary greatly from the entry direction.
(shown as dashed trajectories), the exit direction does not appear to vary greatly from the entry direction.
Contributed by: Paulo D. F. Gouveia (March 2011)
After work by: Paulo D. F. Gouveia, Alexander Plakhov, and Delfim F. M. Torres
Open content licensed under CC BY-NC-SA
Snapshots
Details
The two sections of the curve considered here are similar arcs of two parabolas with the common vertical axis coincident with the line of entry of the cavity and concavities turned toward one another. The optimal configuration can only be achieved when the focus of each one coincides with the vertex of the other (the focal length equals 1).
The authors [1] found this optimal configuration searching for shapes of bodies that maximize Newton’s aerodynamic resistance. But its application does not lie solely in maximization resistance; it can be used in the design of retroreflectors. As can be verified here, the double parabola shape, although it does not guarantee perfect inversion of all the incident radiation, fulfills this function with great success: it gives a good approximation for a significant fraction of the entry angles, and even for the rest, it does not give too great an error. This is very promising for new geometries for optical elements that make up retroreflecting surfaces. See [2] for applications to the automobile industry, including road signs.
References:
[1] P. D. F. Gouveia, A. Plakhov, and D. F. M. Torres, "Two-Dimensional Body of Maximum Mean Resistance," Applied Mathematics and Computation 215, 2009 pp. 37–52.
[2] P. D. F. Gouveia, "Computation of Variational Symmetries and Optimization of Newtonian Aerodynamic Resistance" (in Portuguese), Ph.D. thesis, University of Aveiro, Portugal, February 2008.
Permanent Citation
"A Double Parabola with Retroreflection Properties"
http://demonstrations.wolfram.com/ADoubleParabolaWithRetroreflectionProperties/
Wolfram Demonstrations Project
Published: March 7 2011