Accuracy of Series Approximations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
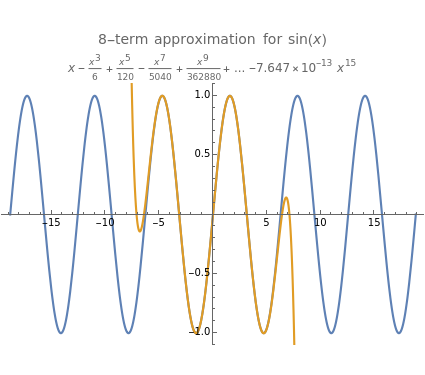
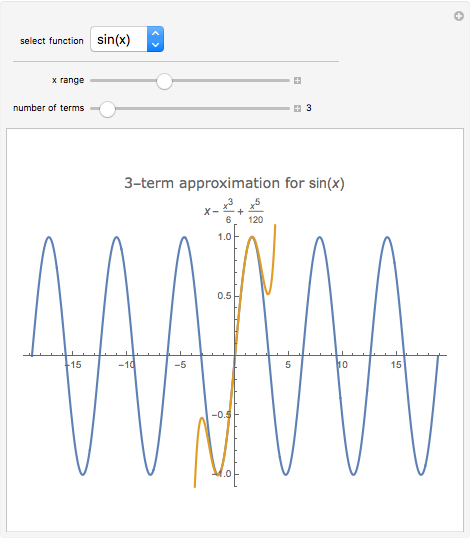
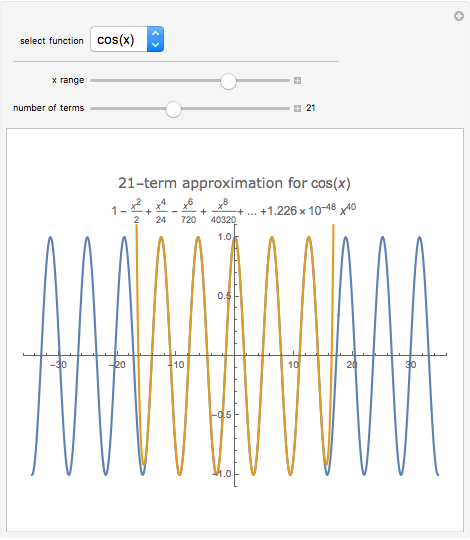
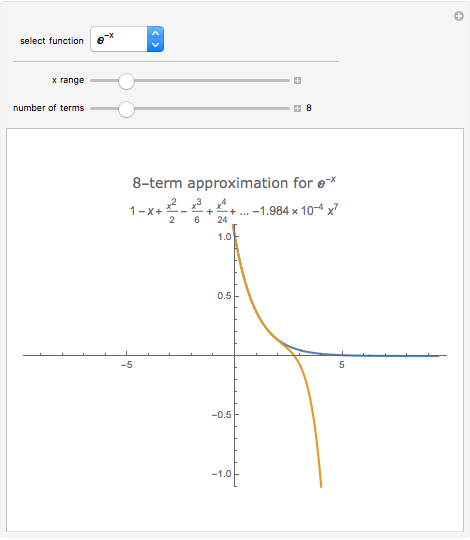
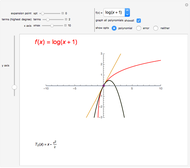
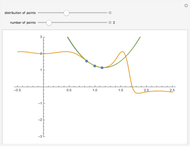
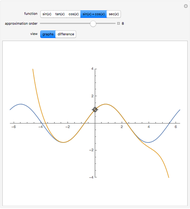
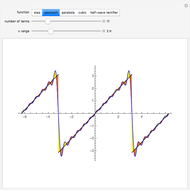
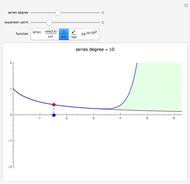
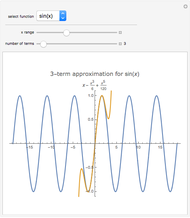
In physics and mathematics, series expansions to approximate functions are often used because using the exact solution is either impossible or involves unnecessary complicated calculations. This Demonstration shows how accurate the series expansions for 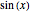 ,
, 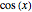 ,
,  ,
, 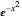 , and
, and 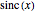 are, and how adding terms increases that accuracy moving away from the origin.
are, and how adding terms increases that accuracy moving away from the origin.
Contributed by: Fred E. Moolekamp III and Kevin L. Stokes (February 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
One of the most common uses of series expansions in physics to simplify calculations is the small angle approximation for the harmonic oscillator, where 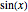 is approximated to x. This makes solving the differential equation much easier but it is not very precise for angles much larger than
is approximated to x. This makes solving the differential equation much easier but it is not very precise for angles much larger than 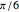 . The coefficient of the last term in the expansion is shown to illustrate just how small it is. Other examples of times a series expansion is used include:
. The coefficient of the last term in the expansion is shown to illustrate just how small it is. Other examples of times a series expansion is used include:
• 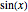 —thin lens equation [1]
—thin lens equation [1]
• 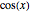 —visibility function (see related links)
—visibility function (see related links)
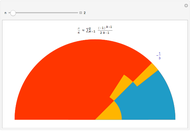
• 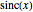 or
or 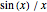 —Euler expanded this series to get an approximation for
—Euler expanded this series to get an approximation for  [2].
[2].
References:
[1] D. Halliday, R. Resnick, and J. Walker, Fundamentals of Physics, 7th ed., Hoboken, NJ: Wiley, 2005 Chapter 34.
[2] W. B. Gearhart and H. S. Shultz, "The Function 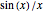 ," The College Mathematics Journal, 21(2), 1990 pp. 90-99 http://www.maa.org/programs/maa-awards/writing-awards/the-function-sinxx.
," The College Mathematics Journal, 21(2), 1990 pp. 90-99 http://www.maa.org/programs/maa-awards/writing-awards/the-function-sinxx.
Permanent Citation