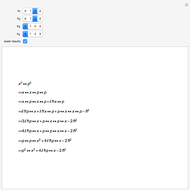
Zeros of Truncated Series of Elementary Functions

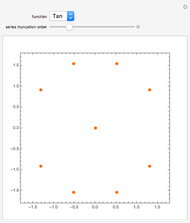
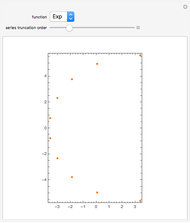
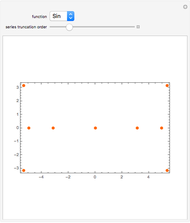
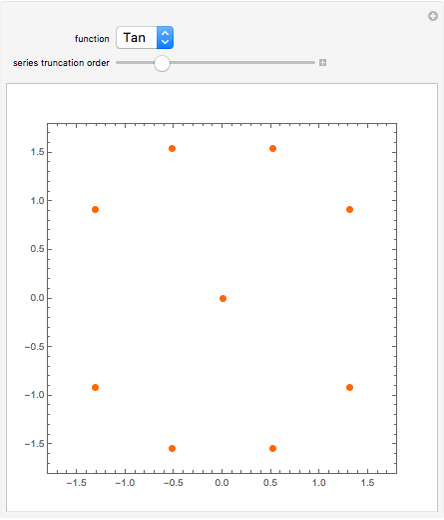
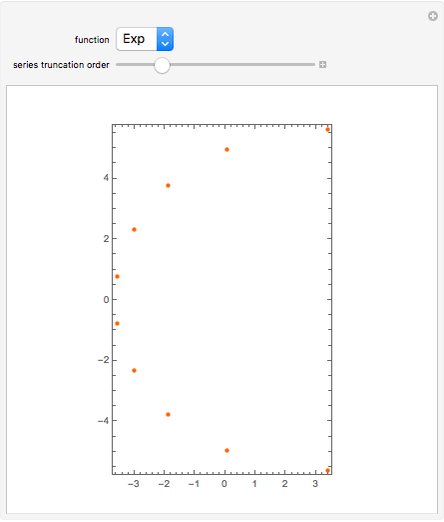
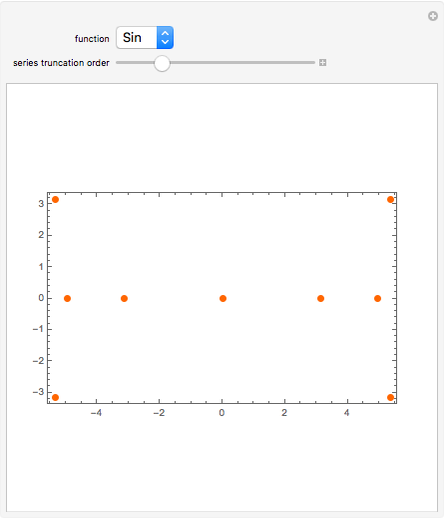
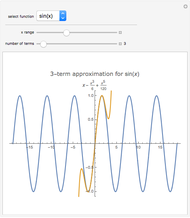
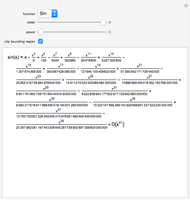
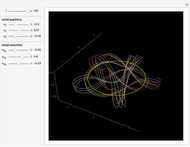
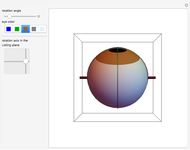
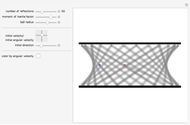
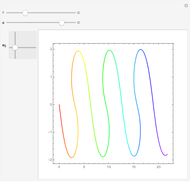
The radius of convergence of a series expansion of a function equals the distance from the expansion point to the nearest singularity of the function in the complex plane. This means that for entire functions, such as the exponential function, sine, and cosine, the radius of convergence of the series is infinite and the zeros of the truncated series approach the zeros of the function. This Demonstration shows the zeros of the truncated series of elementary functions. For functions with singularities in the finite part of the complex plane, such as tangent or cotangent, the zeros must cluster at the circle of convergence.