Area and Volume of n-Dimensional Spheres
Initializing live version
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
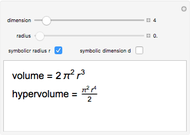
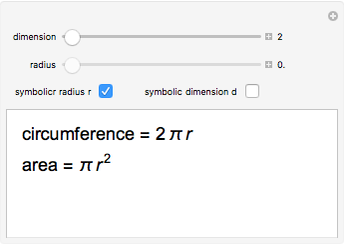
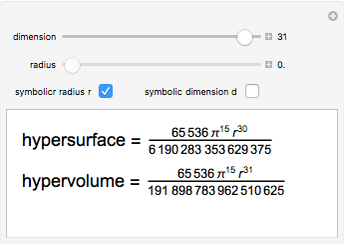
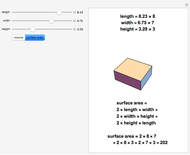
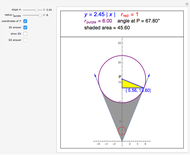
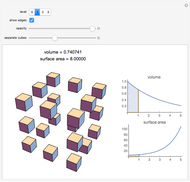
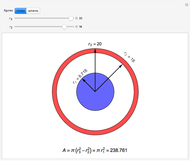
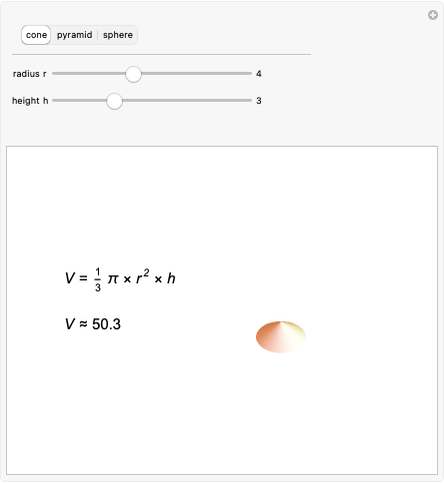
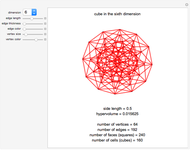
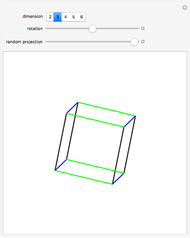
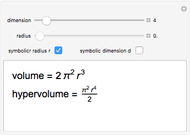
This Demonstration lets you calculate or see the general formulas of the surface area and volume of an 
-dimensional sphere.
Contributed by: Jon Kongsvold (September 2007)
Open content licensed under CC BY-NC-SA
Details
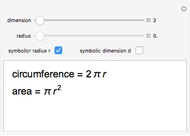
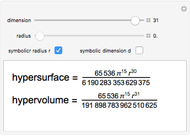
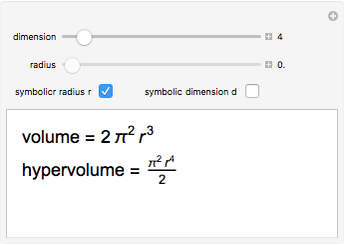
2D 'spheres' are circles and have circumference and area; spheres of dimensions greater than 3 have content for the hypersurface and hypervolume. The skin of a 4D sphere has volume.
Snapshots
Permanent Citation
Related Demonstrations
More by Author
Volume and Surface Area of the Intersection of Two Spheres
Idir Expósito Gómez
The Ratio of Surface Area to Volume for a Cube and a Sphere
Mark D. Normand and Micha Peleg
Estimating the Surface Area and Volume of a Rectangular Prism
Sarah Lichtblau
Volume under a Sphere Tangent to a Cone
Abraham Gadalla
Volume and Surface Area of the Menger Sponge
Sam Chung and Kevin Hur
Rectangles Reasonably Close to a Given Area
Ed Pegg Jr
Equal Cores and Shells in Circles and Spheres
S. M. Blinder
Volume of Cones, Pyramids, and Spheres
Sarah Lichtblau
Geometric Properties of an n-Cube
Andrew Mueller
Rotating Squares, Cubes, and Higher-Dimensional Hypercubes
Michael Schreiber
