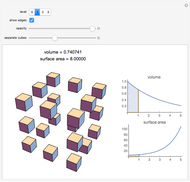
Volume and Surface Area of the Menger Sponge

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
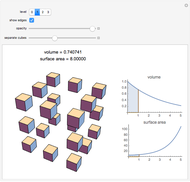
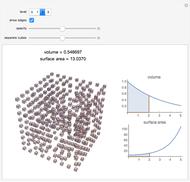
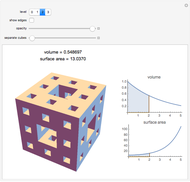
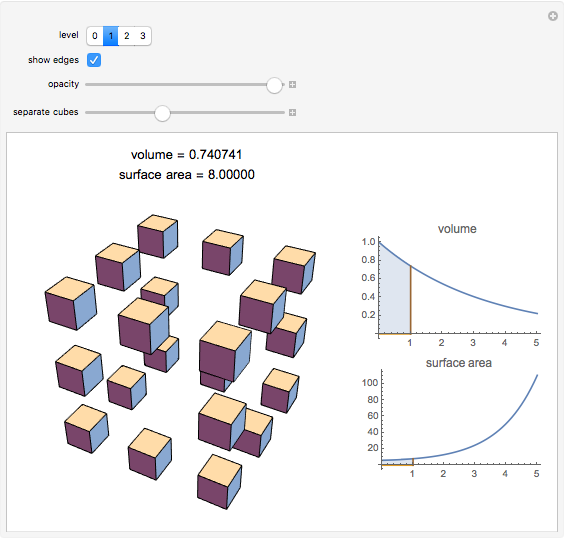
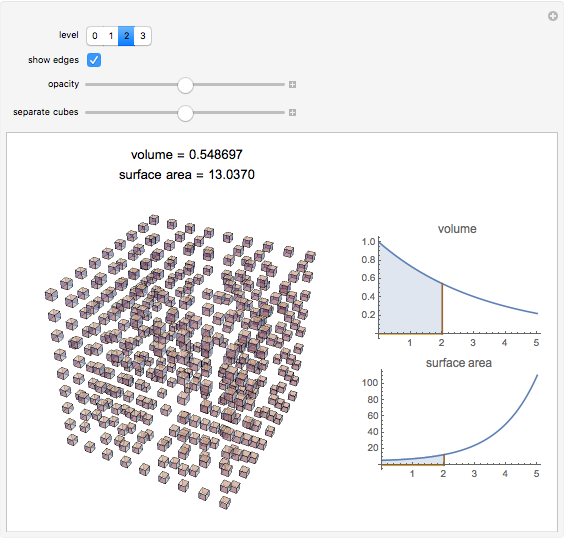
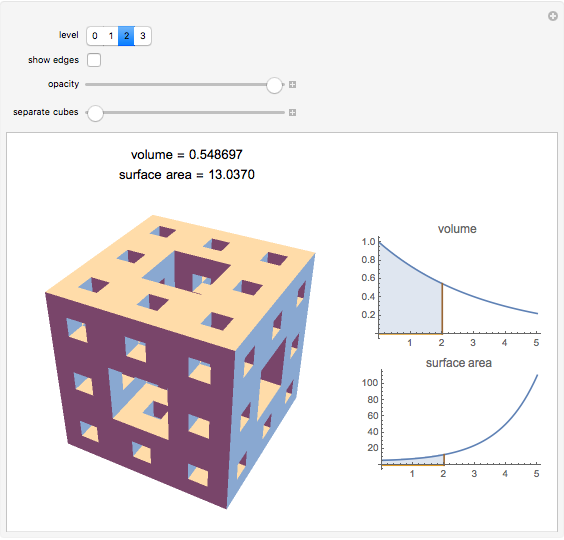
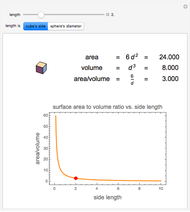
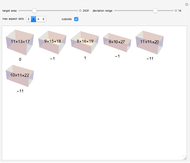
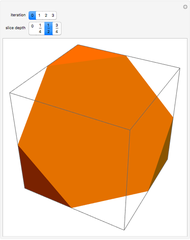
The Menger sponge is constructed by dividing a cube into 27 cubes, then removing the middle cube of each face and the center cube. This process is repeated at each iteration, in the limit creating an object that simultaneously exhibits infinite surface area and zero volume. This Demonstration shows how the surface area of the sponge tends to infinity for each level of the cube while the volume tends to zero.
[more]
Contributed by: Sam Chung and Kevin Hur (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School
Permanent Citation
"Volume and Surface Area of the Menger Sponge"
http://demonstrations.wolfram.com/VolumeAndSurfaceAreaOfTheMengerSponge/
Wolfram Demonstrations Project
Published: June 4 2014