Bead on a Rotating Wire

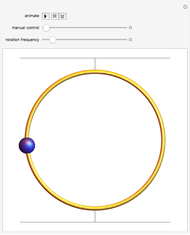
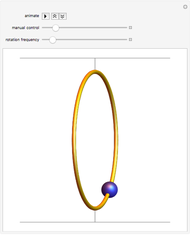
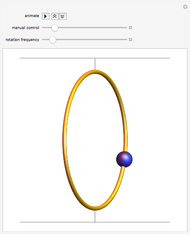
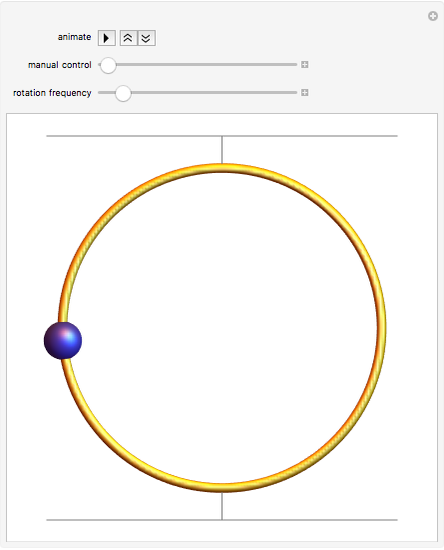
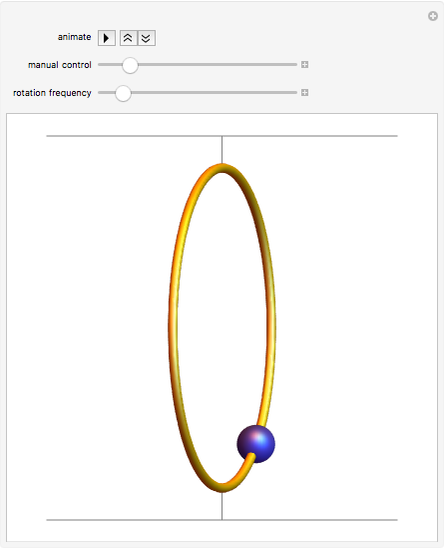
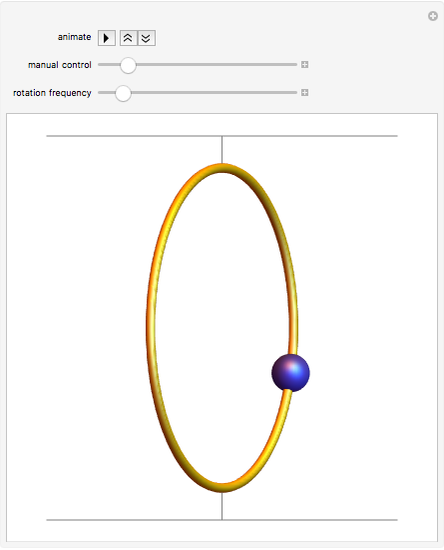
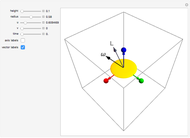
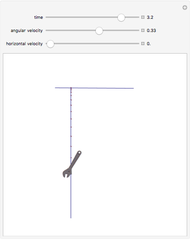
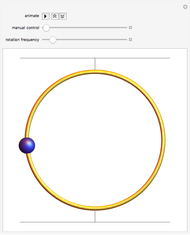
A bead on a rotating wire is a classic problem in the physics subfield of classical dynamics. A circular wire hoop rotates at a constant angular velocity while a bead, constrained to move only on the wire hoop, moves under the influence of gravity. The equilibrium point about which the bead oscillates is initially the south pole of the hoop. As the angular velocity increases, this equilibrium point bifurcates (becoming unstable in the process) into two new equilibrium points which "climb" up the sides of the hoop as the angular velocity increases. The bead now oscillates about one of the new equilibrium points, which is chosen based on the initial conditions.