Rigid Body Pendulum on a Flywheel
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
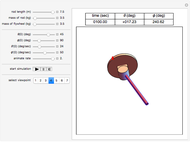
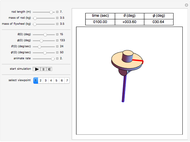
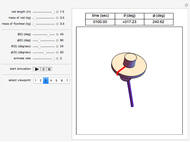
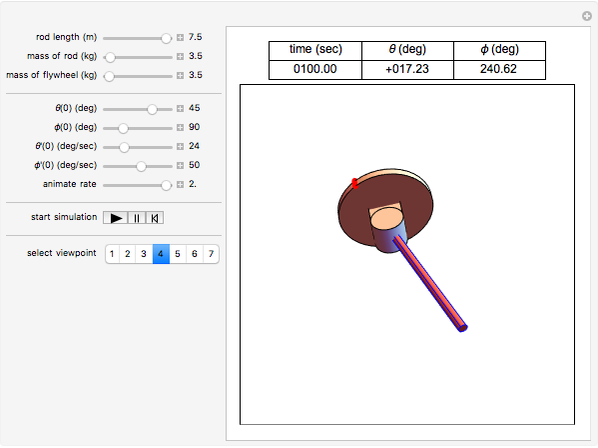
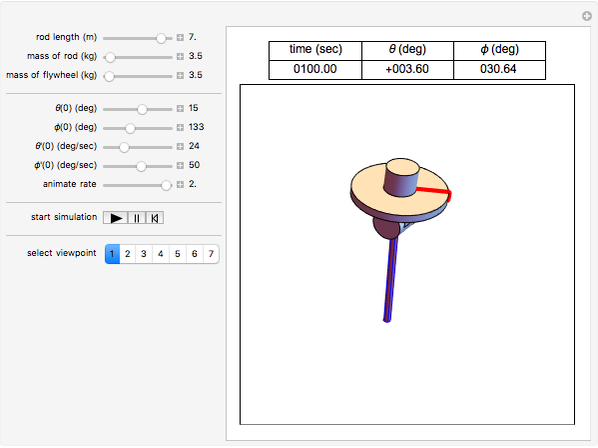
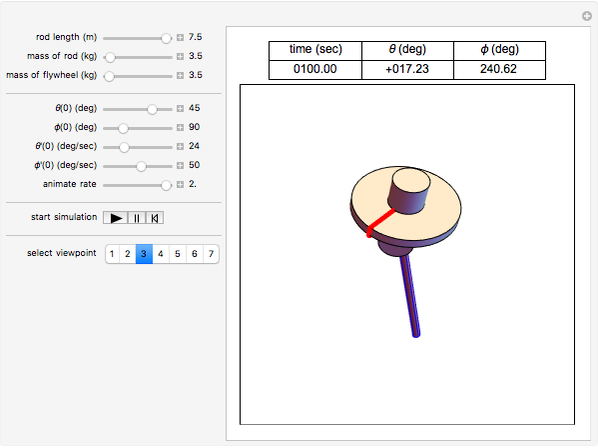
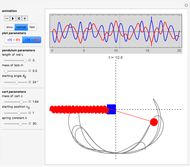
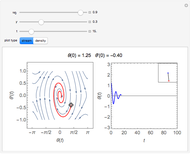
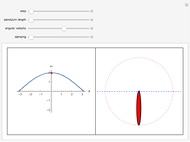
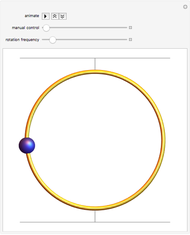
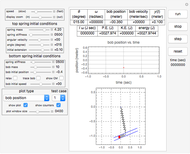
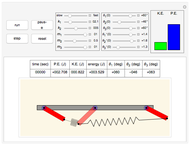
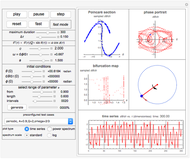
This Demonstration simulates the motion of a rigid pendulum pivoted, with no friction, to a rotating flywheel. The pendulum is forced to spin on its axes by the flywheel's angular motion and at the same it can swing in a fixed 2D plane. The system has two degrees of freedom: 
, which is the pendulum's swing angle, and 
, which is the flywheel's rotation angle. The two nonlinear equations of motion are derived using the Lagrangian energy method. The two equations are solved numerically and the motion is simulated. Interesting motion profiles can be observed by changing the system parameters and the initial conditions.
Contributed by: Nasser M. Abbasi (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
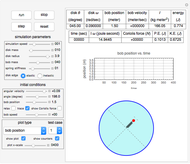
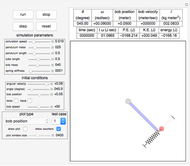
The parameters that you can vary with the sliders are: mass of the flywheel, mass of the pendulum rod, length of the rod, and the four initial conditions needed for the two second-order differential equations. All units are SI.
The pendulum is a rigid body in rotation, assumed to have its center of mass at its midpoint. The equations of motion are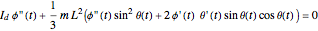 
and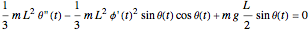 
, where 
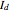is the moment of inertia of the flywheel, given by 
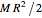, where 
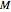is the mass of the flywheel and 
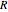is its radius; 
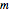is the mass of the pendulum rod and 
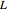is its length. The nonlinear equations are solved numerically using the built-in Mathematica function NDSolve. Notice that the pivot point where the pendulum is attached to the flywheel remains fixed in space.
Permanent Citation
Pendulum Waves
Stan Wagon (Macalester College) and S. M. Blinder
Spinning Disk Pendulum Swinging on Top of a Rotating Table
Nasser M. Abbasi
Double Pendulum
Rob Morris
Bouncing Bob Pendulum
Erik Mahieu
Crankshaft-Driven Pendulum
Erik Mahieu
Pendulum Dangling from a Spring
Erik Mahieu
Spring-Cart-Pendulum System
Erik Mahieu
The Damped Nonlinear Pendulum
Enrique Zeleny
Motion of a Simple Pendulum with Damping
Bartosz Naskrecki
Bead on a Rotating Wire
Ryan K. Smith (Wolfram Research)
-
Heavy Spring with Double Pendulum
Nasser M. Abbasi -
Illustrating the Use of Discrete Distributions
Nasser M. Abbasi -
Dynamic Analysis of a Second-Order System with Harmonic Loading
Nasser M. Abbasi -
Cauchy and Engineering Strain Deformation in 3D
Nasser M. Abbasi -
Dynamics of Two Cylinders with Three Springs
Nasser M. Abbasi -
Principal Stresses and Mohr's Circle for Plane Stress
Nasser M. Abbasi -
Solving the 2D Poisson PDE by Eight Different Methods
Nasser M. Abbasi -
Vibration of a Rectangular Membrane
Nasser M. Abbasi -
Selecting from ImageData Using Rows and Columns
Nasser M. Abbasi -
Three Pendulums Connected by Two Springs
Nasser M. Abbasi -
Wind Tower Structure Represented by Generalized Single Degree of Freedom
Nasser M. Abbasi -
Free Response in a Second-Order System
Nasser M. Abbasi -
Chaotic Motion of a Damped Driven Pendulum: Bifurcation, Poincaré Map, Power Spectrum, and Phase Portrait
Nasser M. Abbasi -
Particle Motion Simulation Using A Priori Collision Detection
Nasser M. Abbasi -
Spring-Mass System on a Rotating Table
Nasser M. Abbasi -
Solid Pendulum with a Spring-Mass System
Nasser M. Abbasi -
Solving the Convection-Diffusion Equation in 1D Using Finite Differences
Nasser M. Abbasi -
Solving the Diffusion-Advection-Reaction Equation in 1D Using Finite Differences
Nasser M. Abbasi -
Solving the 1D Helmholtz Differential Equation Using Finite Differences
Nasser M. Abbasi -
Solving the 2D Helmholtz Partial Differential Equation Using Finite Differences
Nasser M. Abbasi