Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Beating and Roughness

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

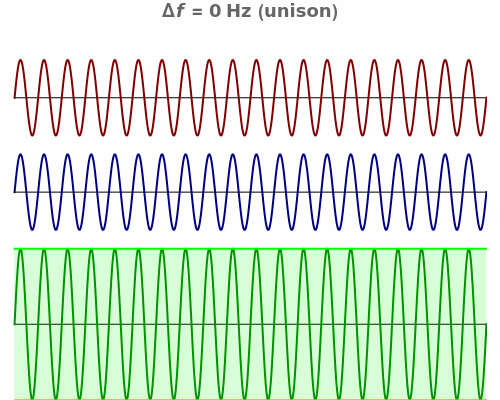
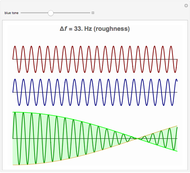
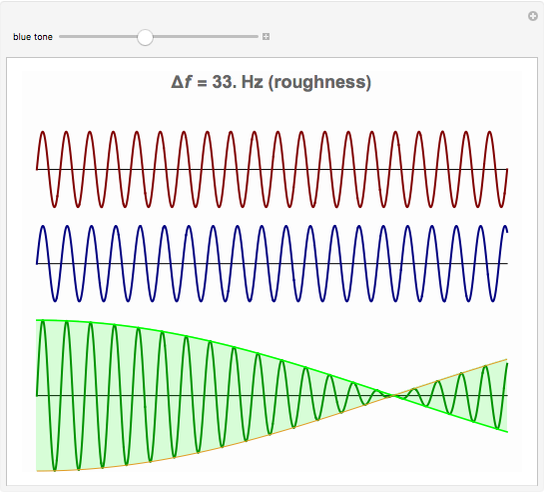
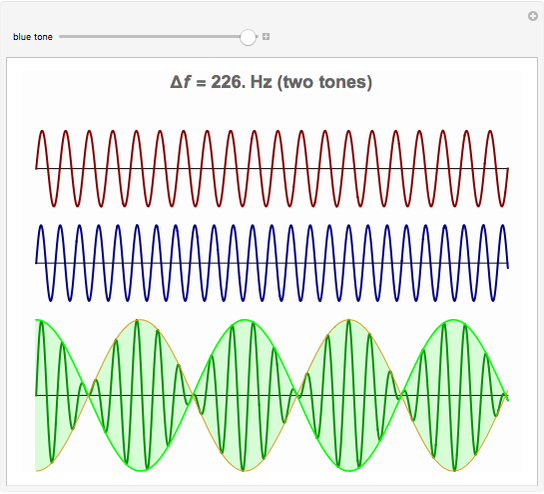
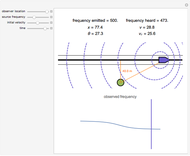
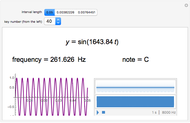
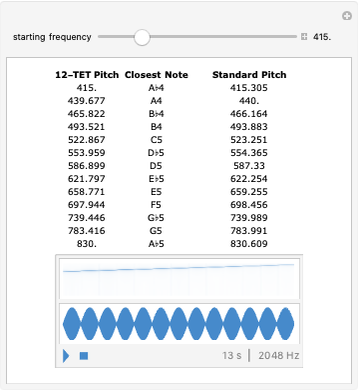
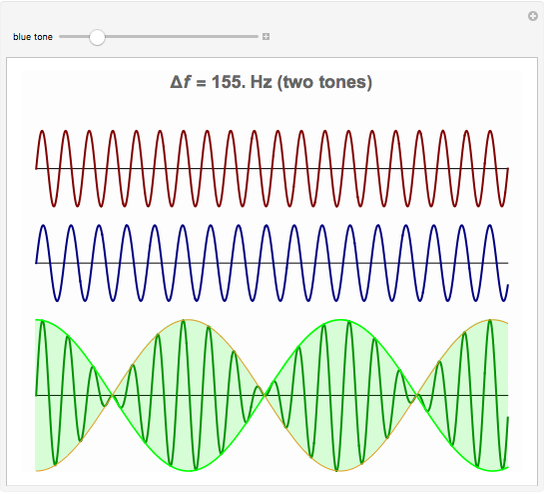
When a pair of beating sinusoids are equal in amplitude, their temporal envelope is characterized by a full-wave rectified sinusoid. This envelope has an oscillation rate at the absolute frequency difference () between the original two sinusoids. If is greater than an auditory filter bandwidth (or critical band), the combination is perceived as two distinct tones.

[more]

Temporal envelope changes produced by amplitude modulation can be perceived as fluctuation strength (or beats) or roughness, depending upon the modulation rate. Fluctuation strength has a maximum at about 4 Hz and roughness peaks at about 70 Hz (see [1]). Roughness tends to disappear when the modulation frequency is greater than 300 Hz. The continuous transition between the two perceptual modes is at about 15–20 Hz. To quantify fluctuation strength and roughness, Fastl and Zwicker proposed the respective units vacil and asper.

[less]

Contributed by: Julian Villegas (March 2011)
Based on a program by: John Kiehl
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] H. Fastl and E. Zwicker, "Psychoacoustics: Facts and Models." Springer Series in Information Sciences, 3rd ed., 22, Berlin: Springer, 2007.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send