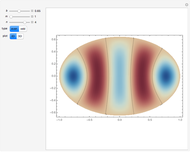
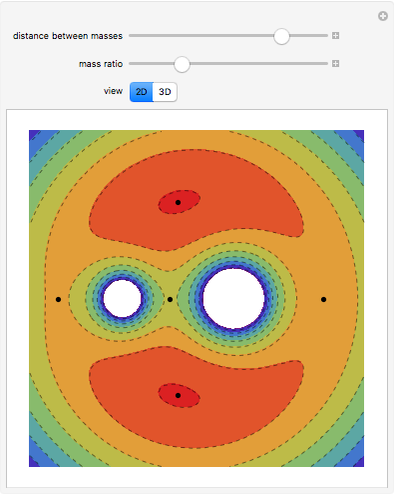
Acoustic Multipoles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
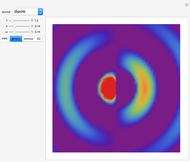
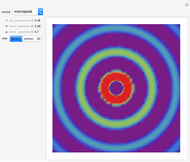
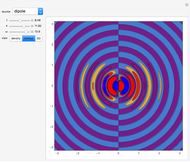
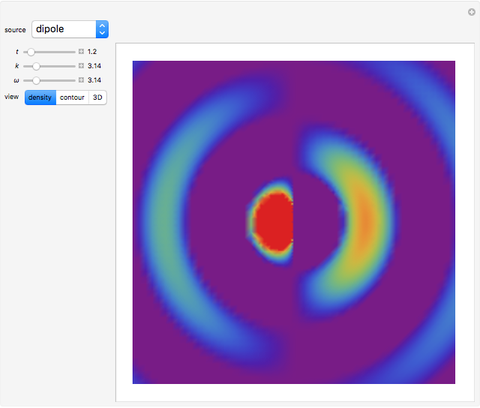
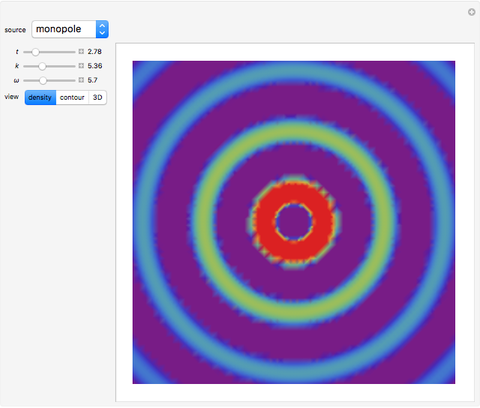
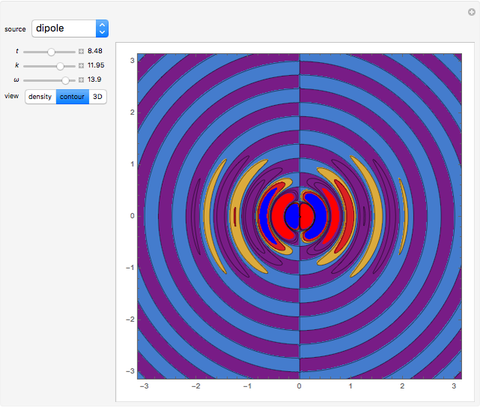
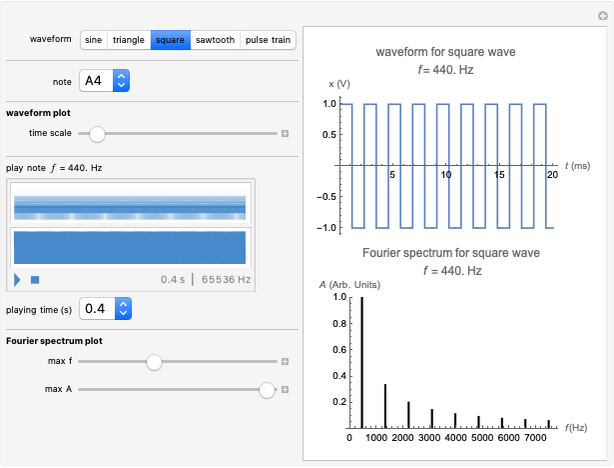
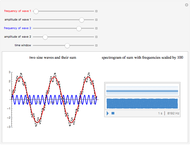
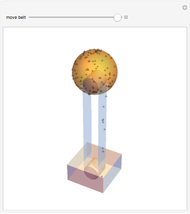
Acoustic waves are produced by successive phases of volume expansion and contraction. In contrast to electromagnetic waves, their polarization is longitudinal. Depending on the number of sources and their geometry, different patterns can be created. The simplest case, with spherical symmetry, is the monopole (e.g. from a boxed loudspeaker). Other common cases are the dipole (from an unboxed loudspeaker) and the lateral quadrupole with four monopoles, with the two pairs out of phase with one other.
Contributed by: Enrique Zeleny (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The solutions can be derived from the acoustic wave equation
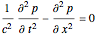 ,
,
where 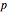 is the acoustic pressure and
is the acoustic pressure and  is the speed of sound.
is the speed of sound.
The simplest acoustic source is the monopole,
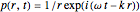 .
.
Taking the spatial derivative of the last expression, for the case of a dipole, we find
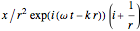 ,
,
and taking the second spatial derivative, for the quadrupole, gives
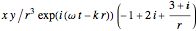 .
.
References
[1] D. A. Russell. "Acoustics and Vibration Animations." (Sep 27, 2013) www.acs.psu.edu/drussell/Demos/rad2/mdq.html.
[2] D. A. Russell, J. P. Titlow, and Y. Bemmen, "Acoustic Monopoles, Dipoles, and Quadrupoles: An Experiment Revisited," American Journal of Physics, 67(8), 1999 pp. 660–664. doi:10.1119/1.19349.
Permanent Citation