Bézier Curve Approximation of an Arc

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
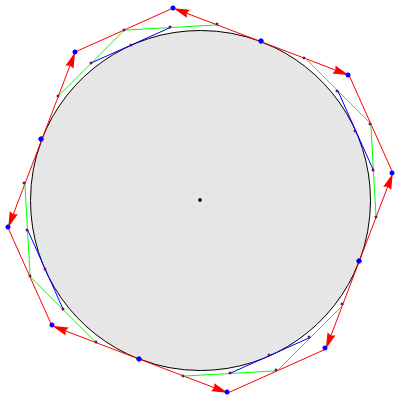
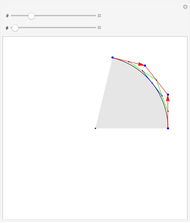
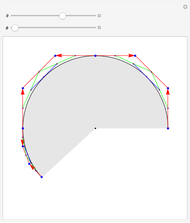
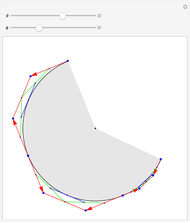
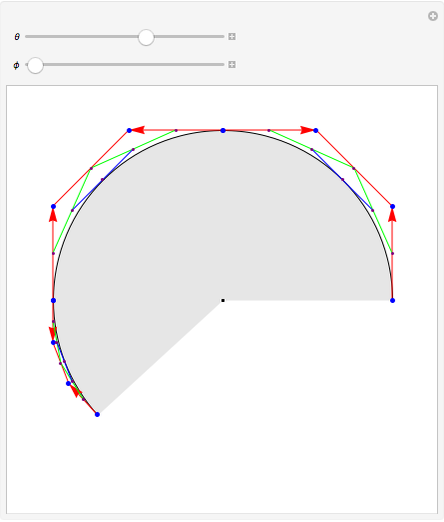
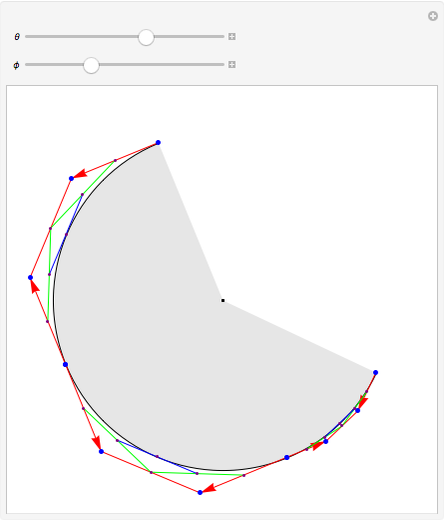
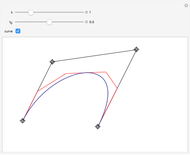
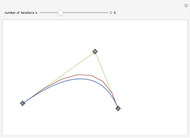
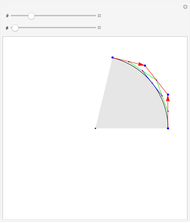
This Demonstration shows how the arcs of a circle can be approximated with 1-4 Bézier curves. Each Bézier curve has four blue control points (two on the arc and two off the arc) with the red arrows pointing from each control point on the arc to the next control point off the arc. The four control points of the Bézier curve can be connected by three red line segments, the midpoints of which can be connected by two additional green line segments; the midpoints of the green line segments can then be connected by one additional blue line segment, which is tangent to the arc at its midpoint.
Contributed by: Rob Raguet-Schofield (May 2007)
Based on work by: Aleksas Riškus
Open content licensed under CC BY-NC-SA
Snapshots
Details
Based on ideas presented in A. Riškus, "Approximation of a Cubic Bezier Curve by Circular Arcs and Vice Versa," Information Technology and Control, 35(4), 2006 pp. 371-378.
Permanent Citation
"Bézier Curve Approximation of an Arc"
http://demonstrations.wolfram.com/BezierCurveApproximationOfAnArc/
Wolfram Demonstrations Project
Published: May 2 2007