q-Bézier Curves
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
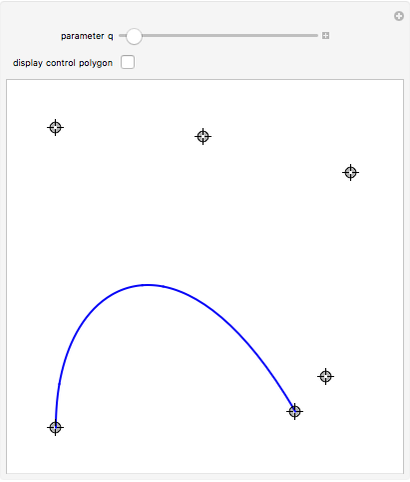
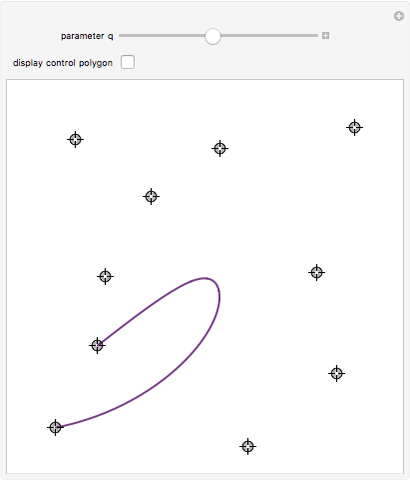
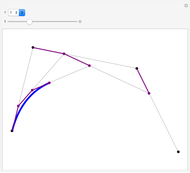
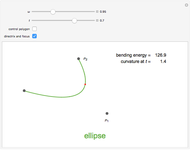
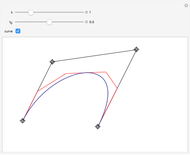
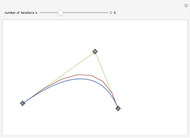
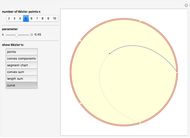
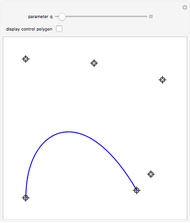
Visualization of Bézier curve and its generalization in 
-calculus. The Bézier curve, introduced by Pierre Bézier, is widely used in computer graphics for modelling smooth curves and also in the design of planes, sport cars, etc. This concept is generalized in -calculus to obtain a whole family of curves parametrized by in the unit interval. The original Bézier curve is then obtained in the limit as goes to 1.
Contributed by: Marko Petkovic (March 2011)
After work by: Predrag Rajkovic and Marko Petkovic
Open content licensed under CC BY-NC-SA
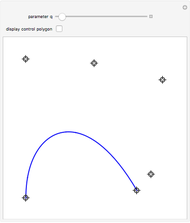
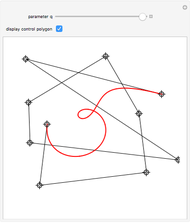
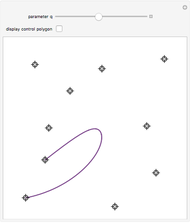
Snapshots
Details
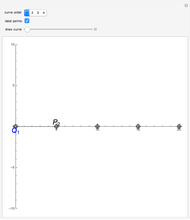
For a given set of control points, 
the Bézier curve is defined by the relation 
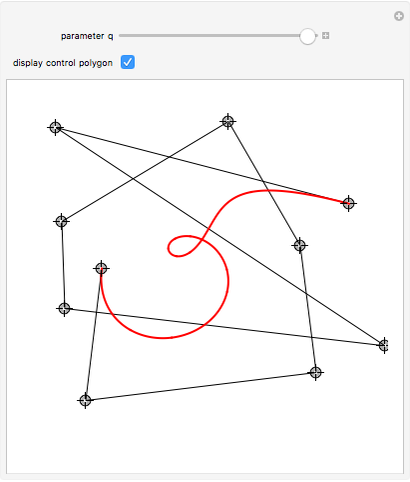
where 
are Bernstein polynomials. Control points form the so-called control polygon. The -calculus generalization of a Bézier curve, called the -Bézier curve, is defined similarly by 
, where the 
are -Bernstein polynomials. This concept was first introduced by G. M. Phillips.
Permanent Citation
Bézier Curve Approximation of an Arc
Rob Raguet-Schofield
Tiling a Path with a Single Trapezoid along a Given Curve
Machi Zawidzki
Bézier Curve by de Casteljau's Algorithm
Bruce Atwood
Focus and Directrix in a Quadratic Bézier Curve
Alexis Luengas Zimmer
Subdivision Algorithm for Bézier Curves
Isabelle Cattiaux-Huillard
Bézier Curve Flowers
Hein Hundal
Raising the Degree for Bézier Curves
Isabelle Cattiaux-Huillard and Gudrun Albrecht
Variation Diminishing Property for Bézier Curves
Isabelle Cattiaux-Huillard
Construction of a Bézier Curve
Justin Chen
Bernstein Polynomials and Convex Bézier Sums
Ludwig Weingarten
