Black-Scholes Option Model


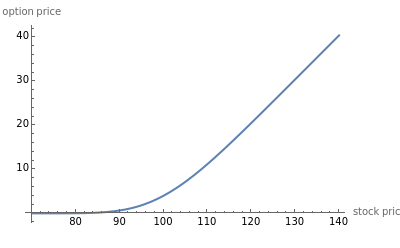
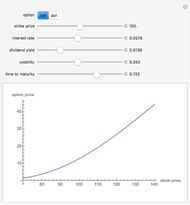
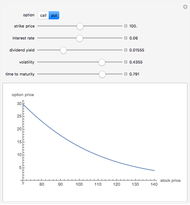
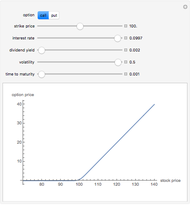
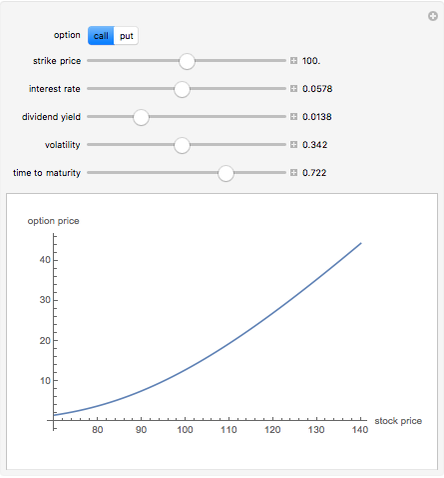
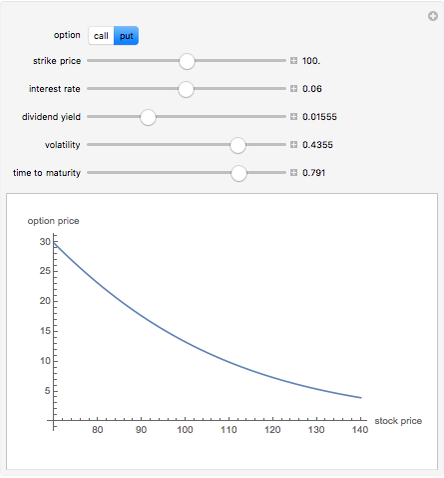
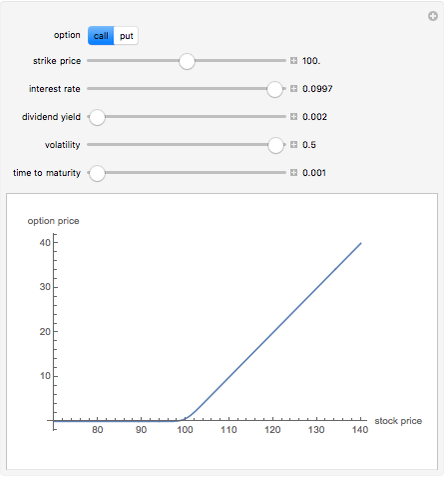
	There are two main types of options that occur in the marketplace: call and put options. These give the option buyer the right to buy or to sell the security, respectively at a later date, called the maturity date, for a fixed price called the strike price. The most popular model for the evaluation of these options is called the Black–Scholes model after its creators. This 2D plot demonstrates how European call and put option prices, determined by the Black–Scholes model, change for different values of their input parameters, which include: current stock price, the strike price, interest rate, dividend yield of the stock, volatility or annualized standard deviation, and time remaining to maturity.


	Contributed by: Michael Kelly (Stuart GSB, Illinois Institute of Technology)
	Show Initialization Code

Snapshot 1: the positive sloping behavior of the call option which a buyer would purchase if he thought that the stock price were going to increase

Snapshot 2: a put option that a buyer would purchase if he thought the stock price were going to fall

The three most important parameters are the stock price, volatility, and time remaining to maturity. Note that for a call, increasing volatility and time while decreasing the strike causes an increase in the option price.