Cardinal Elements of an Aging Human Eye Model with a Gradient-Index Crystalline Lens

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
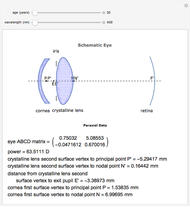
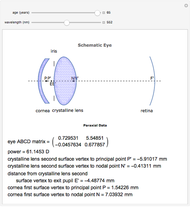
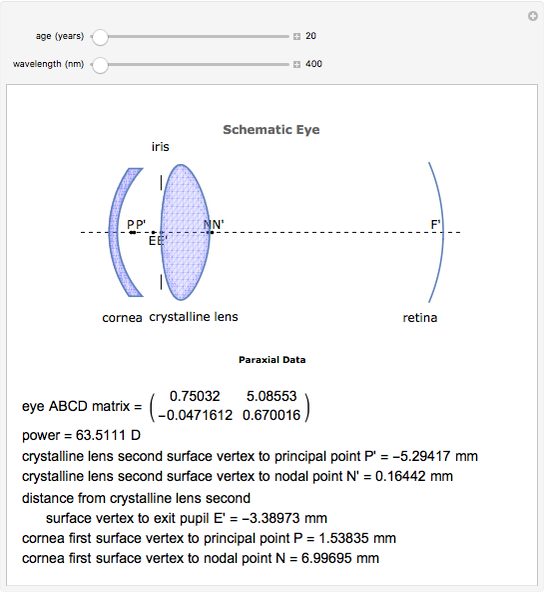
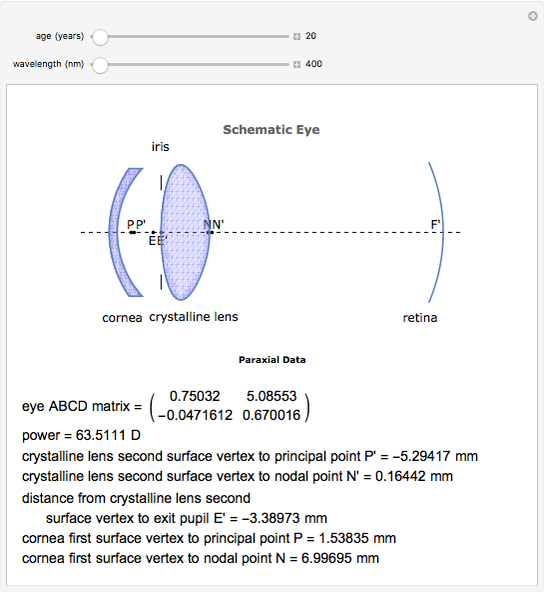
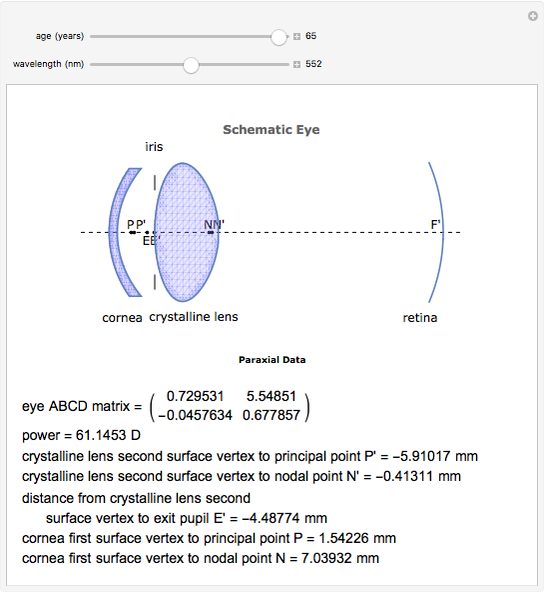
This Demonstration calculates and graphically illustrates the relevant cardinal elements (as a function of the age and the wavelength) of a relaxed emmetropic human eye model having a GRIN crystalline lens.
Contributed by: José A. Díaz,José Fernández-Dorado, Josep Arasa, and Carles Pizarro (June 2009)
Open content licensed under CC BY-NC-SA
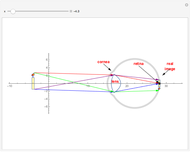
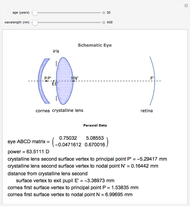
Snapshots
Details
The human eye is an optical system with two components: the cornea and the crystalline lens, with a diaphragm (iris) in contact with the lens. Despite the accommodation process, it is well known that the biometrical data of the human eye changes with age, as does the gradient of the refractive index structure. Therefore, the paraxial properties of the human eye as an optical system evolve with aging. The ABCD matrix formalism has proved to be a good tool to characterize the optical system in the paraxial regime. However, when the optical system has a gradient index element, an ABCD matrix for this element needs to be formulated. Gathering information concerning the aging of the biometric ocular data, a model of the human eye has been created, accurate both anatomically and optically. Together with the ABCD matrix for the GRIN crystalline lens, it is possible to determine the relevant paraxial parameters for the eye model. These parameters—which also vary with the wavelength in the visible part of the electromagnetic spectrum, as the ocular media show light dispersion—help us to study and to teach how the relaxed and emmetropic human eye forms an image on the retina.
A. Gerrard and J. Burch, Introduction to Matrix Methods in Optics, New York: Dover Publishing Inc., 1975.
J. A. Díaz, C. Pizarro, and J. Arasa, "Single Dispersive Gradient-Index Profile for the Aging Human Lens," Journal of the Optical Society of America A, 25(1), 2008 pp. 250–261.
J. A. Díaz, "ABCD Matrix of the Human Lens Gradient-Index Profile: Applicability of the Calculation Methods," Applied Optics, 47(2), 2008 pp. 195–205.