Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Cassini Ovals and Other Curves

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

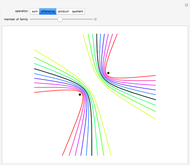
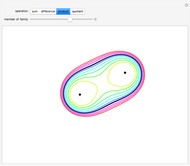
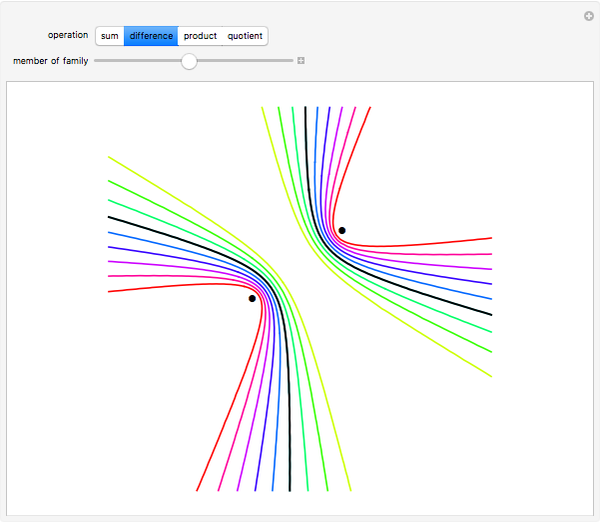
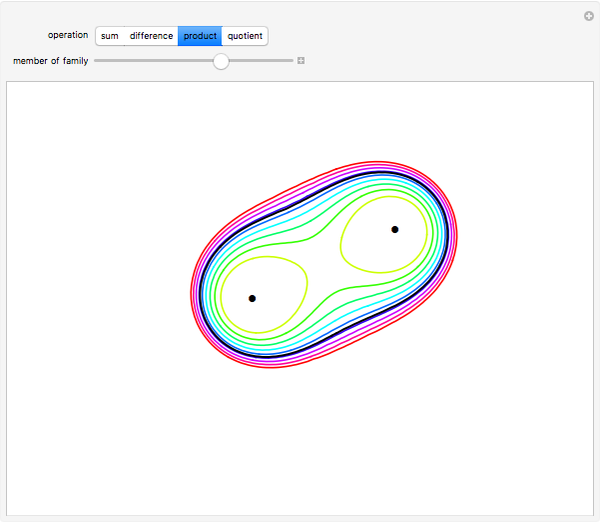
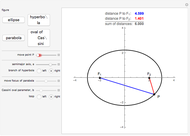
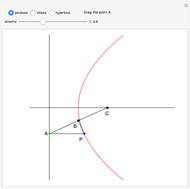
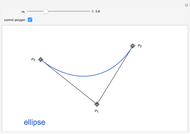
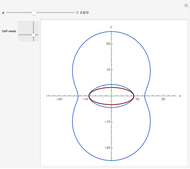
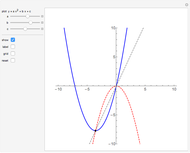
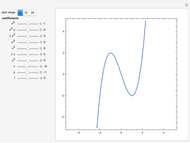
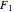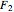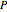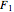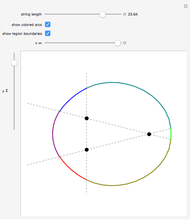
Fix two points and in the plane and consider the locus of a point so that the sum of the distances from to and 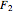equals some constant. For different arithmetic operations (sum, difference, quotient, or product), this set takes on different shapes.

[more]

If the sum of the distances is constant, the shape is an ellipse with foci at the two points.

If the difference of the distances is constant, the shape is a hyperbola with foci at the two points.

If the product of the distances is constant, the resulting family of curves are called Cassini ovals.

If the quotient of the distances is constant, the resulting curves are circles.

The slider controls a value that is proportional to the square of the constant used to determine the black curve.

[less]

Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send