Circular Motion and Newton's First Law

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
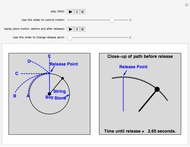
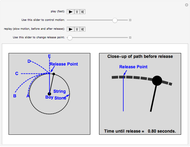
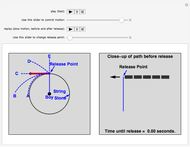
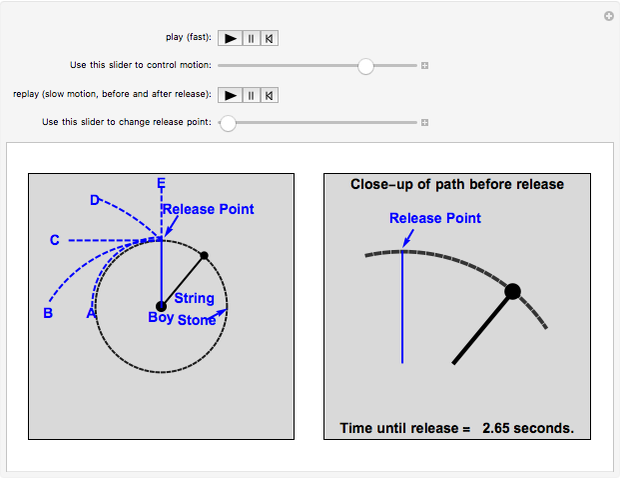
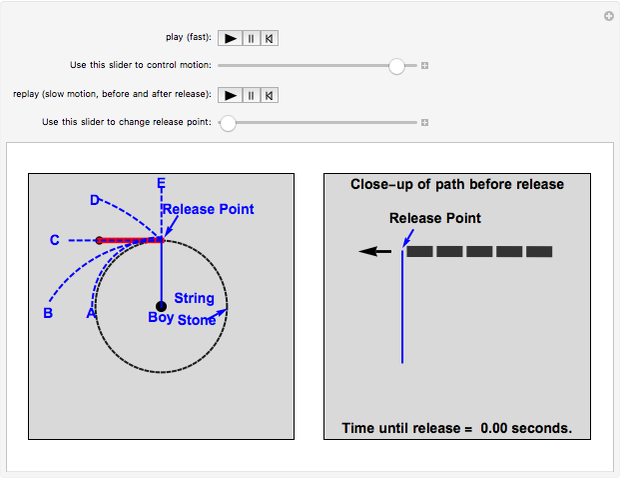
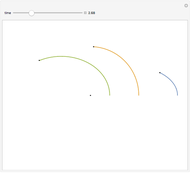
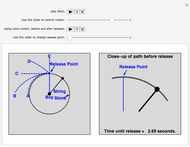
A boy ties a stone to a string and swings it around his head in a horizontal circle. He lets go of the string when the stone is at the "release point."
[more]
Contributed by: Fernand Brunschwig (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
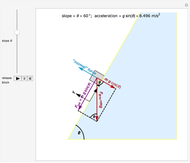
Just on the basis of intuition, most people initially find all of the choices above at least somewhat reasonable. But C is what happens in the "real world". The right panel shows how to visualize this motion so as to understand it better: the curved path becomes straighter and straighter, and after release the stone continues to move along the same straight line path (C). This shows how the second part of the motion "connects with" the first part. The visual model in the right panel is in fact what at least some experts "see" in their minds' eye, and this kind of model is very powerful for thinking about motion. In fact, this Demonstration illustrates the fundamental concept of differential calculus: the "limit", which we explain below.
Newton's First Law of Motion. Isaac Newton's first law of motion applies to the stone's motion after release. The first law says: If all the external influences on an object cancel out (that is, there is zero net external force on the object), the object will move at constant speed in a straight line. (This includes objects at rest; their speed is zero, so with no net external force, they continue to move at zero speed.) After the stone is released, it is no longer interacting with the string, and it then moves in a straight line at constant speed (as seen from above).
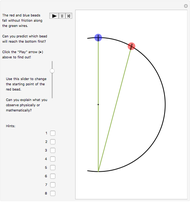
Newton's First Law and "Intuition." The first law and the way the stone moves after it is released seem to contradict certain "intuitive" ideas about circular motion. For example, the stone might tend to "remember" the fact that it was previously moving in a circle. As a result, it seems reasonable that the stone would move along path A or B. On the other hand, if we focus on the fact that the pull on the string by the boy towards the center of the circle keeps the stone moving in a circle at a constant distance from the boy at the center, it seems reasonable that once that pull disappears, the stone would move away from the center, along path D or E.
This Demonstration illustrates that neither of these ideas, despite their intuitive reasonableness, are in accord with what happens in the real world. Understanding this situation fully involves developing one's physical intuition and learning how to visualize and think in a new way. The right panel shows how at least some experts visualize and think about this situation.
Applying Newton's First Law. Understanding the physics of motion involves developing an intuition and a set of principles, such as the first law of motion, which help us understand what we observe. To understand more clearly how to apply the first law, visualize the change in the position of the stone in the millisecond just before it is released (as in the right panel): during that time interval, the stone moves along a very short segment of the circle toward the left. That little piece of the circle does not curve very much, and if we imagine the time interval before release gradually getting shorter, that piece of the circle also gets shorter, and straighter. We can never make the time interval zero, but we can make it as short as we wish. As the time interval before release approaches zero, the stone's motion during that interval approaches an extremely short, horizontal straight line directed toward the left. As a result, after release, the stone simply continues this motion, in accordance with the first law, along the extension of the tiny straight line (path C).
An example of a limit. A limit is a quantity that continues to change as time goes on, but it changes less and less and gradually approaches a definite value. For example, as the time to release gets shorter, the path of the stone changes less and less, but it keeps changing, gradually approaching a straight line tangent to the circle. We can make the path as straight as we wish by choosing the time to release sufficiently short. But we can never in fact get to an absolutely straight path, because if we make the time to release zero, the length of the path is also zero. This can seem to be a paradox, and it makes thinking about this situation difficult. In fact, for much of human history, before Newton and Leibniz, such thinking seemed impossible. However, as Newton and Leibniz demonstrated in the process of inventing the differential calculus, a "limit" such as this does exist—it is possible to think about—and calculate—the speed and direction of motion of the object at the exact time of release, or, in fact, at any time.
Direction of motion of an object moving along any curve. As illustrated in the right panel, the "limit" of the direction of motion at any instant of an object moving in a circle is a straight line tangent to the circle at the point where the object is located. In fact, this idea is not limited to objects moving in a circle: for an object moving along any curve, the limit of the direction of motion at any instant is a straight line tangent to the curve at the point where the object is located. As required by Newton's first law, if all the external influences on the object suddenly cancel out or are removed, the object will then travel in the direction of the tangent to the curve, in a straight line.
Inspired by Chapter 15, Section 2 of R. Karplus, Introductory Physics: A Model Approach, 2nd ed., Boston: Captains Engineering Services, 2003.
Permanent Citation
"Circular Motion and Newton's First Law"
http://demonstrations.wolfram.com/CircularMotionAndNewtonsFirstLaw/
Wolfram Demonstrations Project
Published: March 7 2011