Hooke's Law

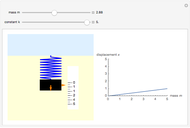
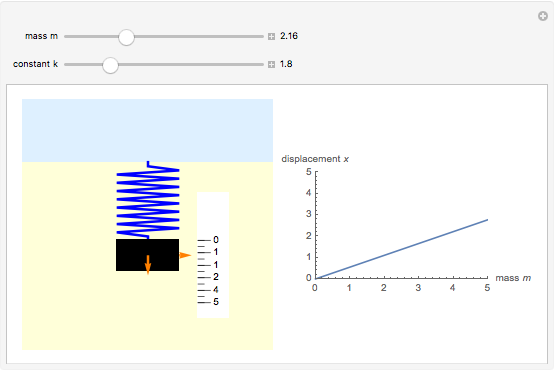
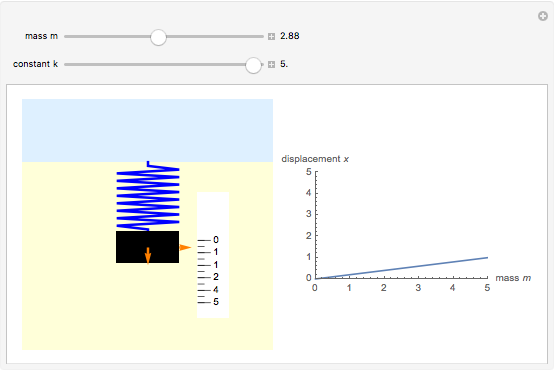
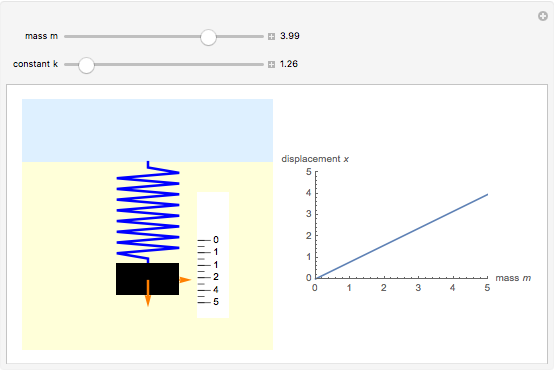
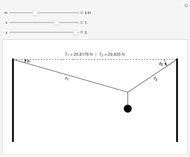
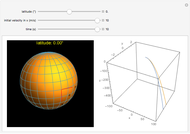
For a spring, the deformation (strain) produced by a force (stress) is proportional to the force applied, as long as its elastic limit is not exceeded, so the spring can return to its original shape after the force is removed. Thus , where is the force due to the weight of the mass , is the displacement from the equilibrium position, and is the force constant, depending on the material used, the number of windings, and so on. The deformation can also be a compression, for negative . The plot on the right shows displacement as a function of mass for fixed .

This law was discovered in 1676 by the British scientist Robert Hooke.