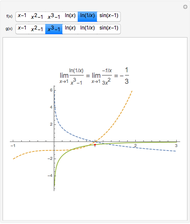
Confidence and Prediction Bands

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
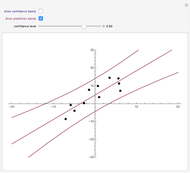
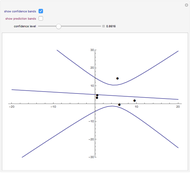
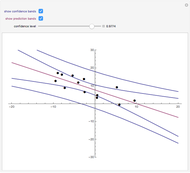
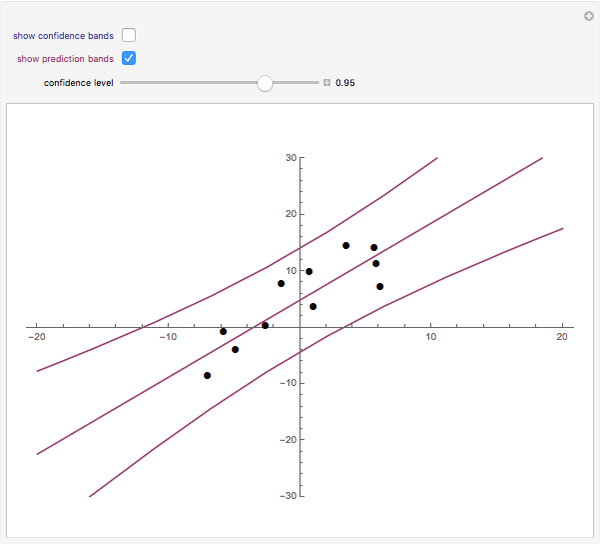
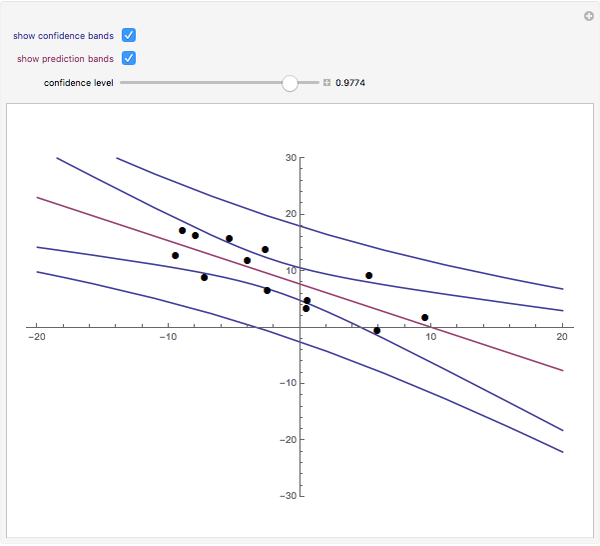
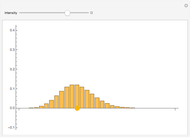
Drag the points or alt-click the plot to add or subtract points from the dataset. The least-squares regression line for the dataset is shown, as well as the option to include confidence or prediction bands with a confidence level that you can adjust with the slider.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The least-squares regression line is the line that best fits a bivariate dataset in the sense of minimizing the sum of the squares of the vertical distances from each point in the dataset to the line. Denote the points in the dataset (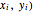 . Assume that
. Assume that 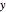 follows a normal distribution whose mean is a linear function of
follows a normal distribution whose mean is a linear function of  (with unknown slope and intercept) and whose standard deviation is a constant function of
(with unknown slope and intercept) and whose standard deviation is a constant function of  . Then a confidence interval for the expected value of
. Then a confidence interval for the expected value of 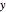 can be constructed using standard techniques. As the expected value of
can be constructed using standard techniques. As the expected value of 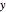 is a function of
is a function of  , the endpoints of this interval will be as well. When plotted as a function of
, the endpoints of this interval will be as well. When plotted as a function of  , these endpoints form "confidence bands" between which runs the regression line.
, these endpoints form "confidence bands" between which runs the regression line.
A confidence interval for the 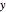 value associated with a new
value associated with a new  value (as opposed to a confidence interval for the mean of all such
value (as opposed to a confidence interval for the mean of all such 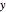 values) is called a prediction interval. Its endpoints are also functions of
values) is called a prediction interval. Its endpoints are also functions of  , which when plotted form "prediction bands". As individual
, which when plotted form "prediction bands". As individual 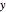 values vary more than their mean, the prediction bands are wider than the confidence bands.
values vary more than their mean, the prediction bands are wider than the confidence bands.
Permanent Citation