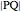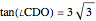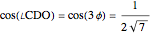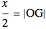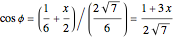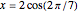Constructing a Regular Heptagon Using Gleason's Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
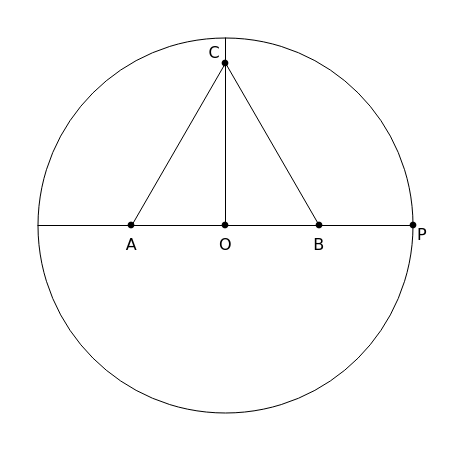
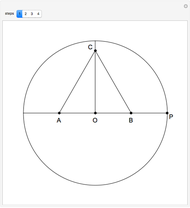
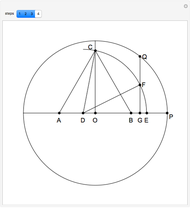
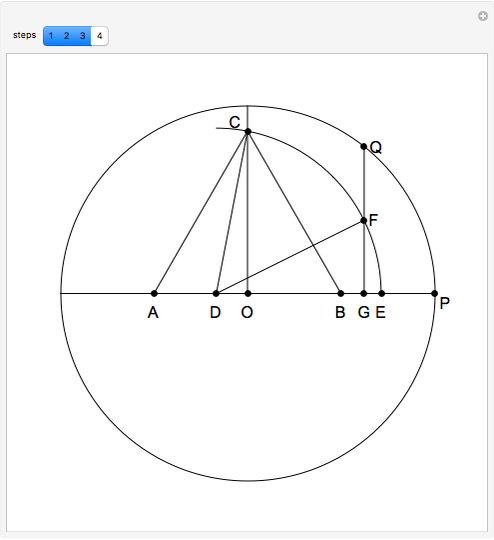
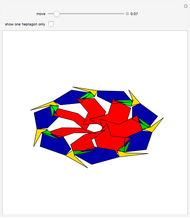
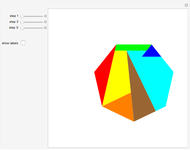
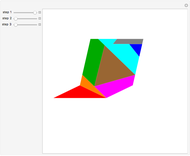
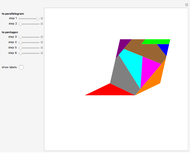
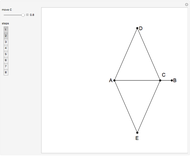
This Demonstration shows Gleason's method for constructing a regular heptagon, using the following steps:
[more]
Contributed by: Izidor Hafner (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
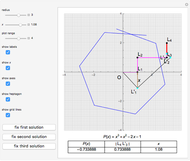
The points of a regular heptagon inscribed in the circle of radius 1 are given by 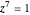 . Since
. Since 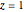 is a solution, divide the polynomial
is a solution, divide the polynomial 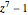 by
by  to get
to get
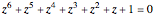 .
.
If
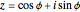
then
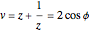 .
.
Substitute 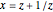 to get the third-degree equation
to get the third-degree equation
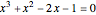
with solutions
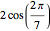 ,
,
 ,
,
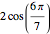 .
.
These solutions also follow from the trigonometric identity
 .
.
Set  and
and 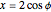 to get
to get
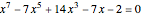 ,
,
which factors as
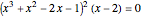 .
.
Reference
[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998 p. 45.
Permanent Citation