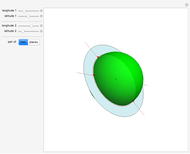
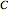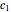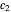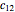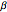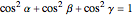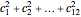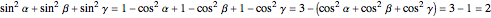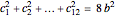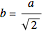Sum of the Squares of the Sides of a Projected Regular Tetrahedron
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
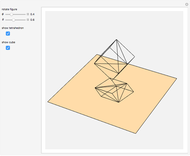
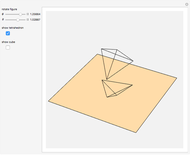
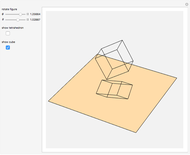
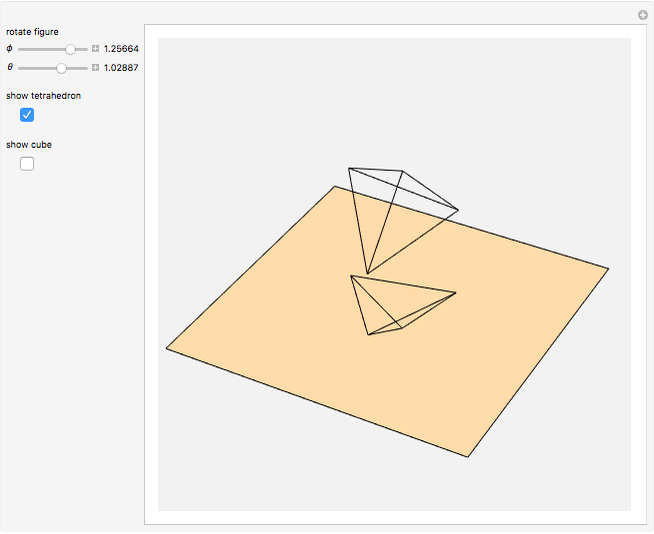
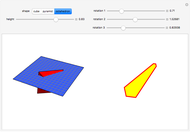
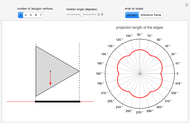
Let  be a regular tetrahedron with side
be a regular tetrahedron with side  . Project
. Project  orthogonally to a plane
orthogonally to a plane 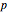 and let
and let 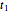 ,
, 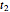 , …,
, …,  be the lengths of the projections of the six sides of
be the lengths of the projections of the six sides of  in
in 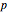 . This Demonstration shows that
. This Demonstration shows that  .
.
Contributed by: Izidor Hafner (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This problem was posed in [1, pp. 20, 28].
Reference
[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.
Permanent Citation