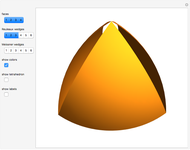
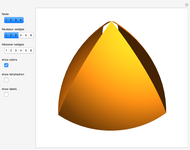
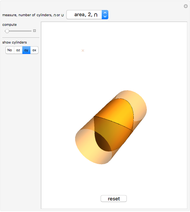
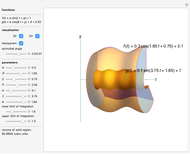
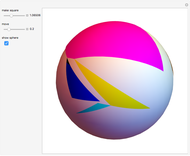
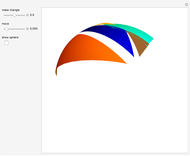
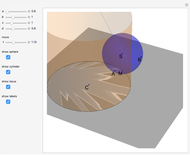
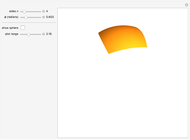
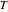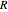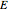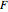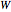Meissner Tetrahedra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
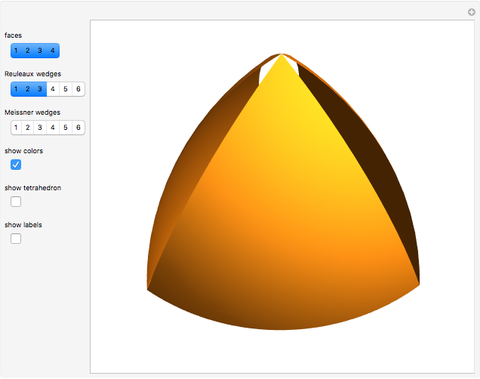
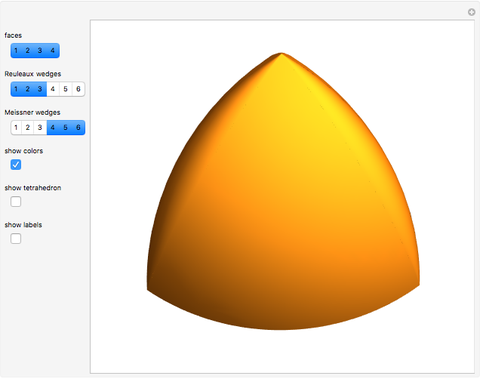
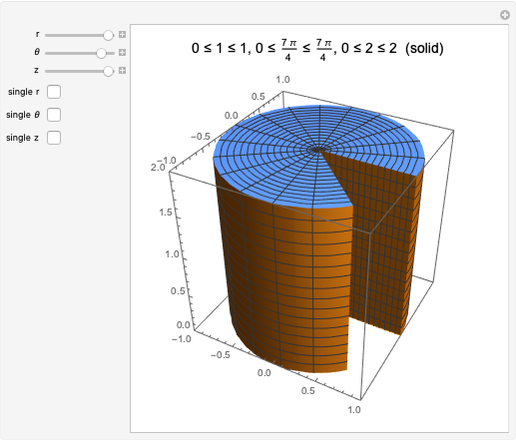
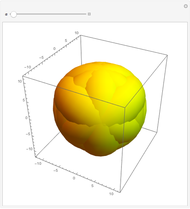
The two Meissner bodies are solids of constant width. Others are spheres and certain solids of revolution.
[more]
Contributed by: Izidor Hafner (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] B. Kawohl and C. Weber. "Meissner's Mysterious Bodies." (Jun 19, 2011) www.mi.uni-koeln.de/mi/Forschung/Kawohl/kawohl/pub100.pdf.
[2] E. Meissner, "Über Punktmengen konstanter Breite," Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich, 56(42–50), 1911. www.archive.org/stream/vierteljahrsschr56natu# page/n53/mode/2up.
[3] E. Meissner and F. Schilling, "Drei Gipsmodelle von Flächen konstanter Breite," Zeitschrift für angewandte Mathematik und Physik, 60(92–94), 1912.
Permanent Citation