Constructing A Simple Optical System

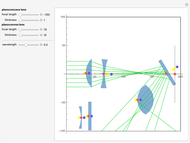
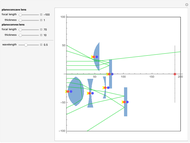
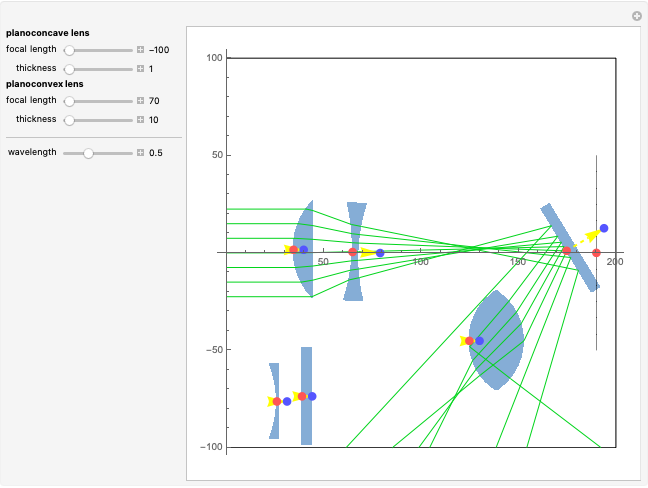
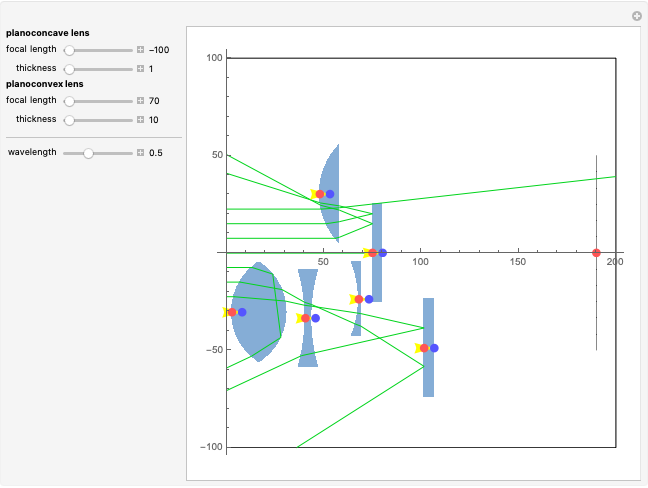
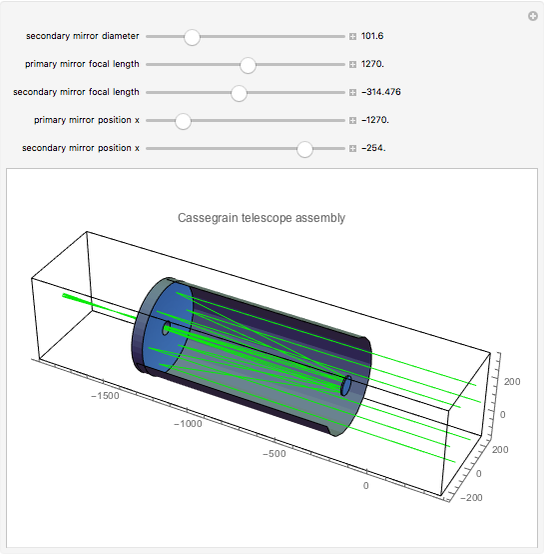
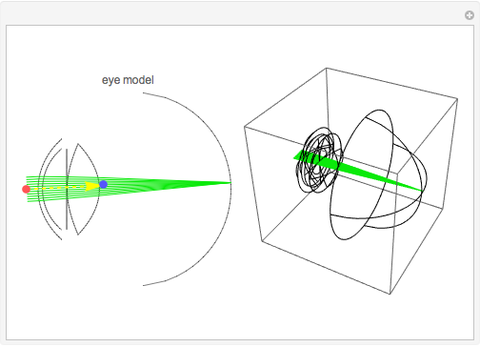
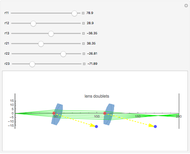
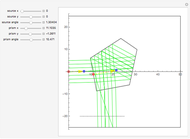
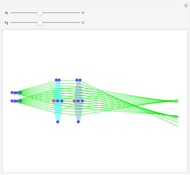
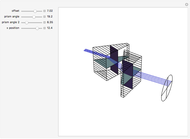
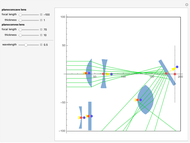
The planoconvex and planoconcave lenses assume a component medium of BK7 glass. Users may change the focal length and thickness with the sliders. Press the "+" next to the sliders for more details. The biconvex lens has a fixed focal length of 39 mm, an aperture of 50.8 mm with thickness of 28 mm, a design wavelength of 0.589 microns, and assumes a quartz medium. The biconcave lens has a focal length of -100.515 mm, an aperture of 50 mm, a thickness of 5 mm, and a fused silica medium. Move the lens components directly using the red and blue locators. 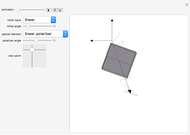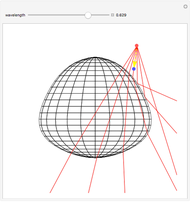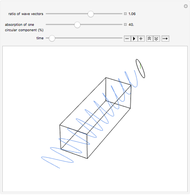The red locator moves the components in the - plane. The blue locator rotates the elements. Pull out the blue locator arrow for finer rotation. Try moving optical elements in and out of the path of light. The optical assembly that is shown consists of lines of rays, a light source, a planoconvex lens, a planoconcave lens, a biconvex lens, a biconcave lens, two mirrors, and a screen. Users can also change the wavelength of the light source using the slider. This particular Demonstration assumes a visible light range of .4 to .7 microns.