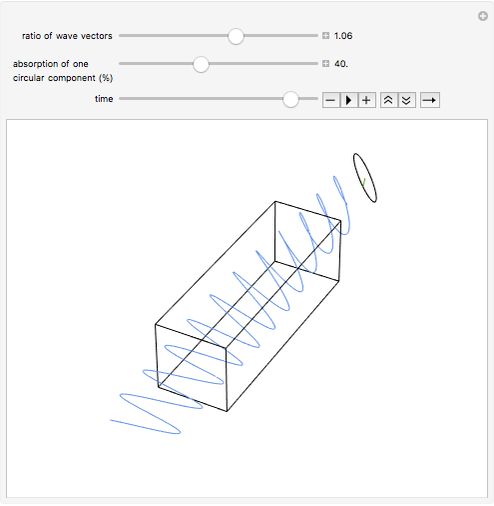
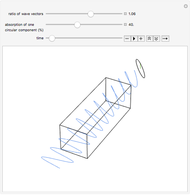
Circularly polarized light waves (or, in general, electromagnetic waves) can be constructed as a superposition of two linearly polarized light waves of the same frequency with perpendicular planes of polarization, equal amplitudes, and a phase shift of one quarter of a wavelength. Depending on the sign of the phase shift the resulting wave is a left- or right-hand circularly polarized wave.
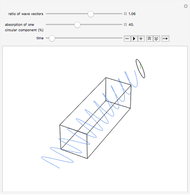
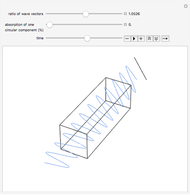
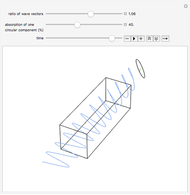
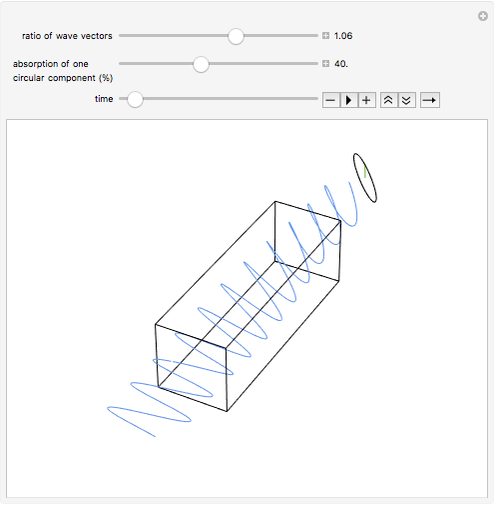
In turn, a linearly polarized light wave can be constructed from a superposition of a left- and a right-hand circularly polarized wave. The plane of polarization depends on the phase shift between the two circularly polarized components. We can use this behavior to explain the phenomenon of optical rotation. Consider a medium, indicated in the animation by the rectangular box, that is chiral. For example, in chemistry one has a solution of a chiral compound with some enantiomeric excess. The medium interacts slightly differently with the left- and the right-hand circular components of a linearly polarized light wave. (The electric field vector goes around on a left- or right-handed helix that can also be considered chiral.) These different interactions cause the refractive indices for the circular components to be slightly different, slowing down one of the circular components more than the other as they enter the medium. As the linearly polarized wave passes through the medium, the phase shift increases between the two circular components, which manifests in a rotation of the plane of polarization of their superposition.
The animation is constructed in exactly this way. The electric field vector for the incoming linearly polarized wave, in blue, is constructed as a superposition of left- and right-hand circularly polarized components. You can adjust the ratio of the wave vectors for the left- and right-hand circular components. The more the ratio deviates from unity, the larger the optical rotation angle becomes. As you can see, the rotation angle is also proportional to the path length that the light wave takes through the chiral medium. There is a symbolic "detector" that traces the amplitude of the outgoing wave at a fixed position.
If the chiral medium also absorbs light, then the amplitude ratio of the two circularly polarized components changes, in addition to the change in their relative phase. The medium exhibits circular dichroism, that is, the absorption coefficients for the circular components are slightly different. A percentage absorption can be selected in the animation for one of the circularly polarized components relative to the other over the full path length. For simplicity, the animation is constructed such that the first component is not absorbed at all. Also, the Demonstration assumes that a simple linear decrease of the amplitude has been applied instead of the exponential decrease according to Beer's law. The result is an outgoing wave that not only has its plane of polarization rotated but is also elliptically polarized. In the case of 100% absorption you can see the single remaining circularly polarized component. The amount of ellipticity, which is proportional to the medium's circular dichroism, is also shown by the detector.
The animation, qualitatively, models what goes on inside a polarimeter. Note that the dimensions (wavelengths versus cuvette size, etc.) are not to scale! We suggest pausing the animation between rotations because it is quite CPU intensive.
[less]