Cylinders through Five Points

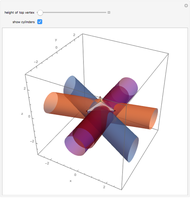
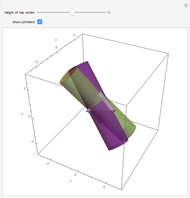
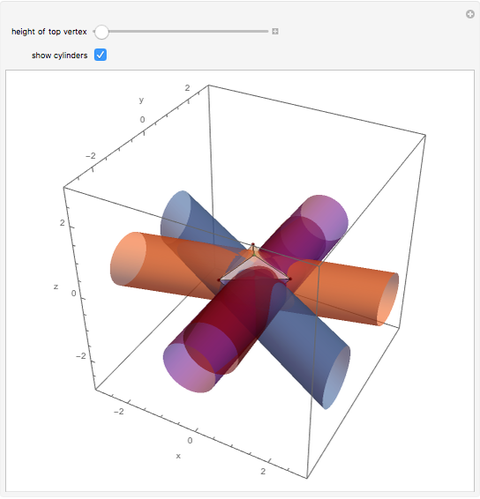
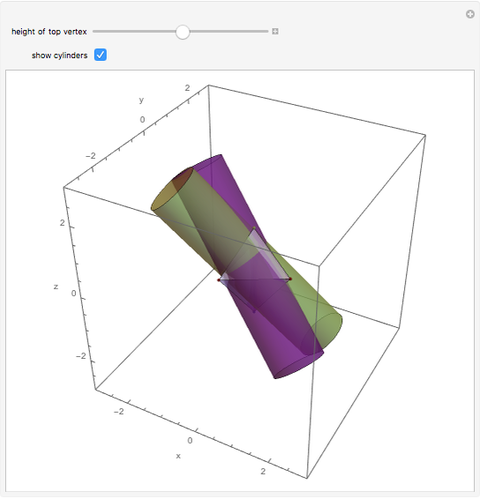
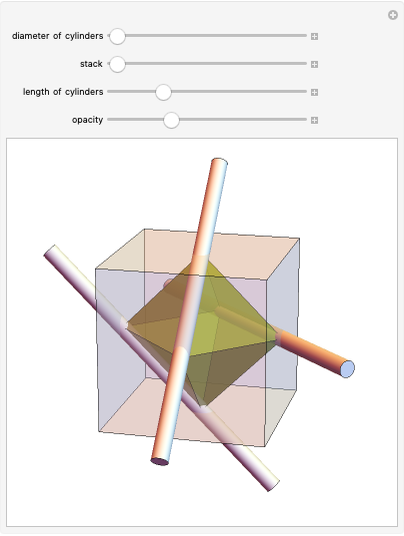
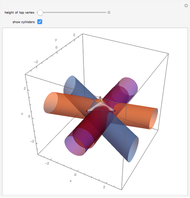
Given five points there are, in general, at most six cylinders containing them. There are six solutions to the set of equations that describe the radius and axis parameter values (counting multiplicity), but some of these solutions may be complex valued. In the special case where the points are the vertices of two regular tetrahedra glued together along a common face, there are in fact six real valued solutions. The tetrahedra are oriented so that the glued face is in the horizontal plane, and the top vertex is allowed to move up or down. At a certain value, which is 5/4 times its initial value, the six cylinders will coalesce into three pairs (that is, the solutions each have multiplicity two). Beyond that value the cylinders "disappear;" that is, all solutions become complex.