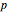Mathematica MathWorld Wolfram Science More »

HOME

TOPICS

LATEST

Data Compression Using Asymmetric Numeral Systems


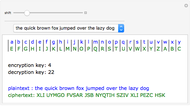
	This Demonstration allows you to experiment with compression using a new method: asymmetric numeral systems. Using a probability distribution , a sequence of symbols of a given length is generated and encoded using the parameters of the encoder. The decoding table, starting from a given state, produces a symbol and new state, with blue bits added to get the new state in the range. A summary is on the right: the optimal asymptotic minimum bit per symbol required (Shannon's entropy), how it should be asymptotically compressed with an ideal compressor but using no necessarily optimal (=) probability distribution, and how it compares with the generated example. Next you see the distribution of symbols in the table, the generated sequence, and finally the correlations in encoded sequences of bits.


	Contributed by: Jarek Duda

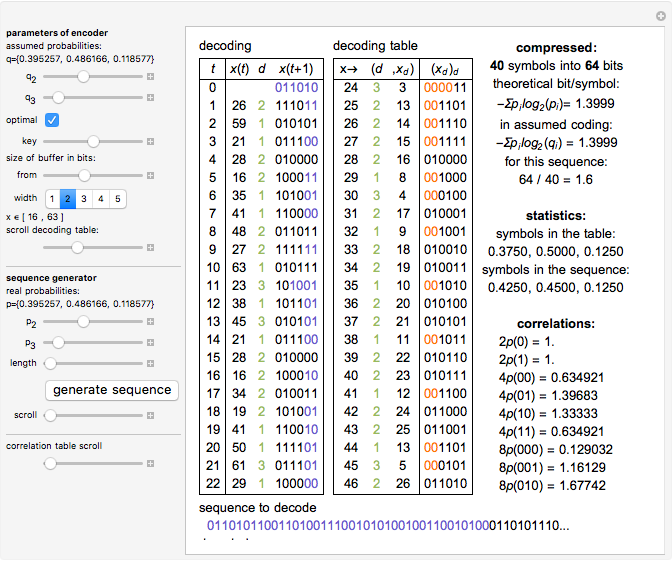
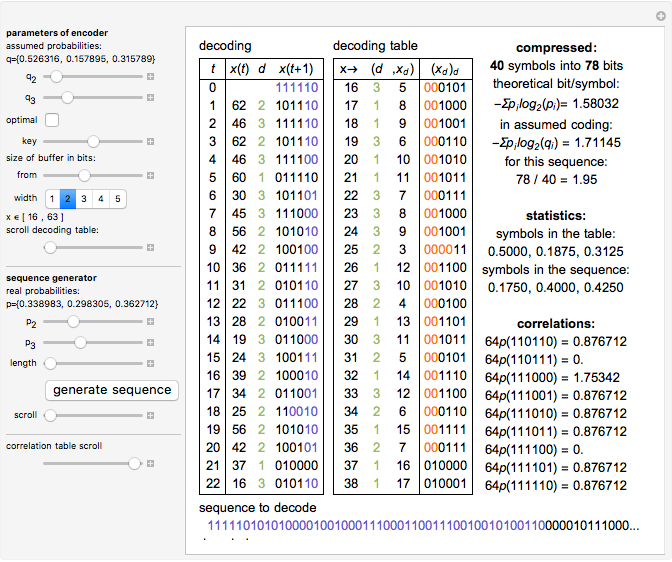
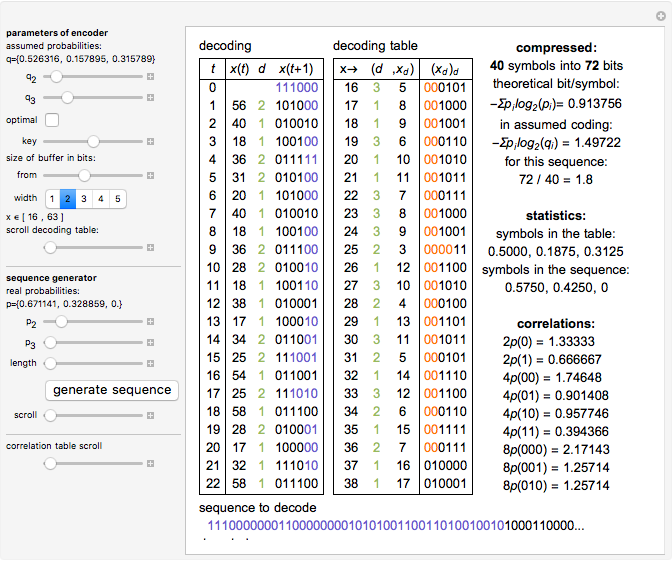
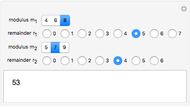
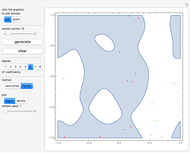
Numeral systems are optimal for encoding sequences of symbols (digits) that have uniform distribution.

An asymmetric numeral system is a generalization constructed to be optimal for any given probability distribution

of symbols (digits).

With some information stored in a natural number

, to add some information stored in a digit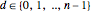

that all has the same probability (

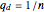), take

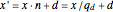to place this information in the right-most bits.

In the asymmetric case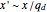

should hold asymptotically.

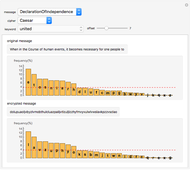
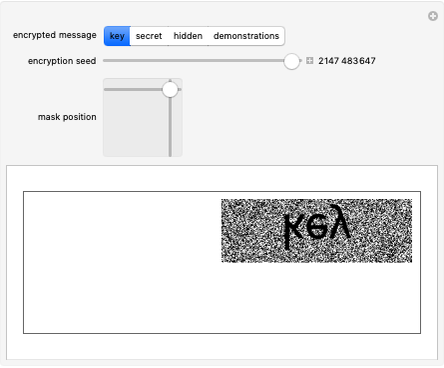
This cannot usually be done exactly, but for asymptotic behavior the symbols only need to be distributed uniformly. A random number generator can be used to choose a specific distribution. If this generator is initialized with a given key, this additionally encrypts the output.

To encode in this way,

would grow to infinity. To prevent that,

is restricted to some range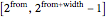

and some bits are removed in blocks of "width" bits to a bit stream (compressed file).

Basic information about this coding can be found in:

http://arxiv.org/pdf/0710.3861

More information about using it in cryptography:

http://arxiv.org/abs/0902.0271

Cryptography (Wolfram MathWorld)

"Data Compression Using Asymmetric Numeral Systems" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/DataCompressionUsingAsymmetricNumeralSystems/

Contributed by: Jarek Duda

Mathematica 7 Just Released--Get Mathematica Player 7 Free--Download Now

Cryptography

Browse all topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom