Decomposing a Regular Polygon with an Odd Number of Sides into Rhombuses and Triangles
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
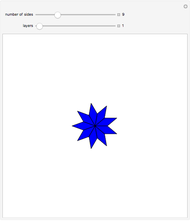
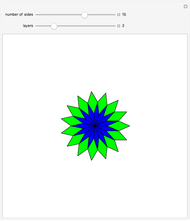
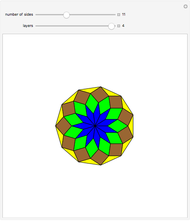
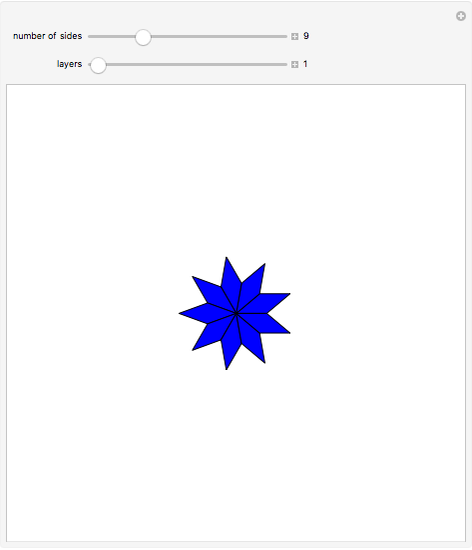
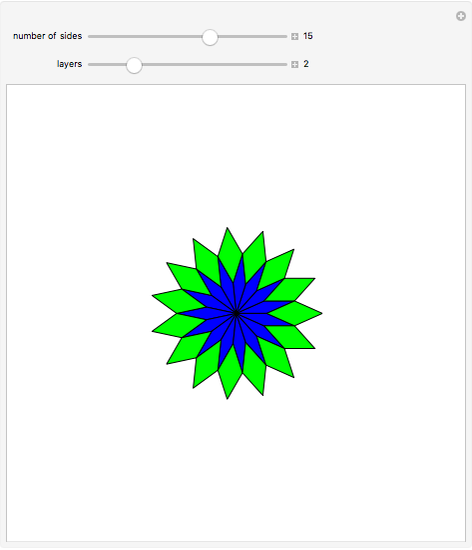
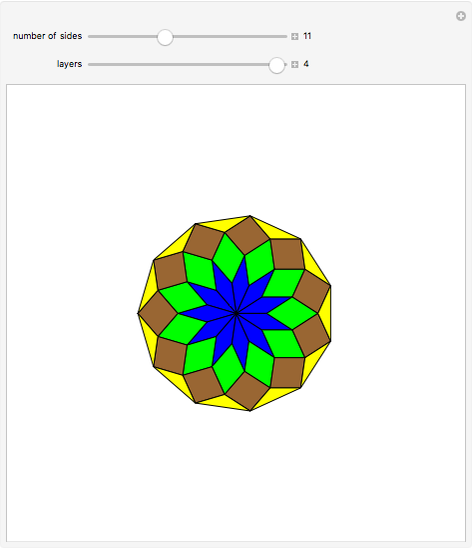
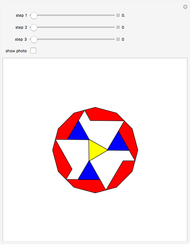
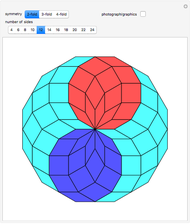
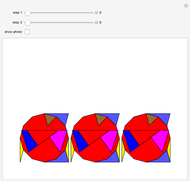
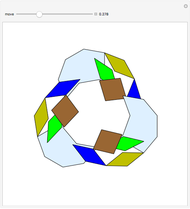
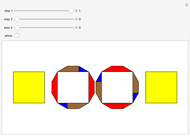
A regular polygon with an odd number of sides can be decomposed symmetrically into rhombuses and triangles.
Contributed by: Izidor Hafner (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 2002 p. 193. www.cs.purdue.edu/homes/gnf/book.html.