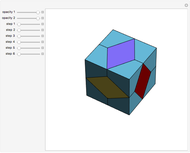
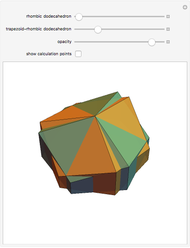
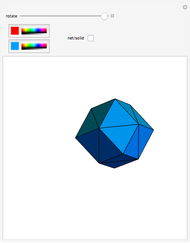
Dissection of a Cube to a Quarter of a Rhombic Dodecahedron of the Second Kind

Initializing live version

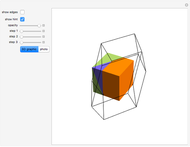
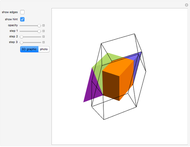
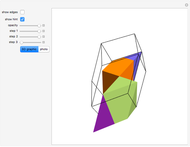
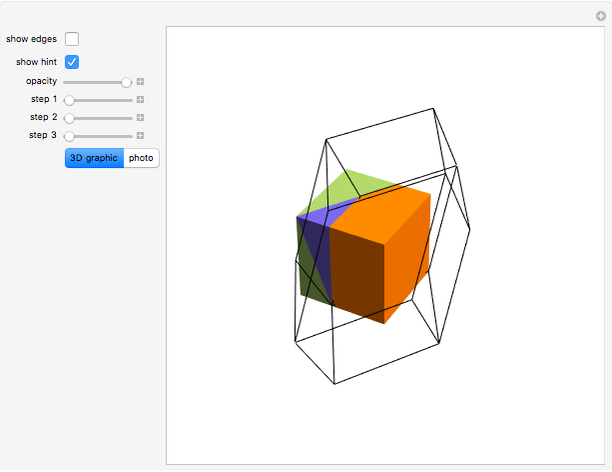
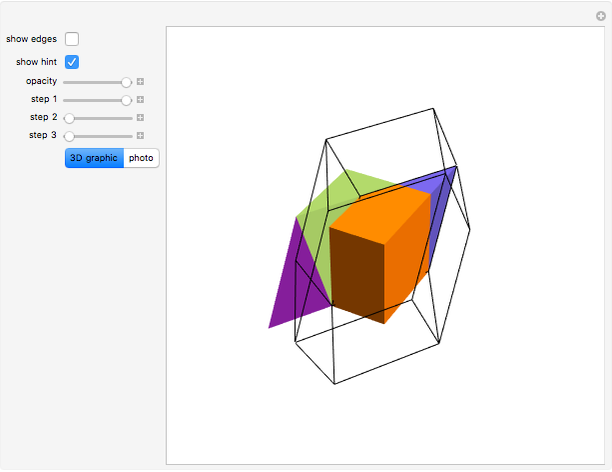
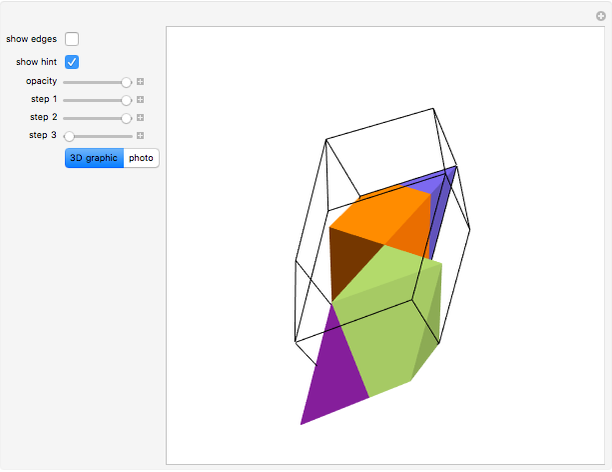
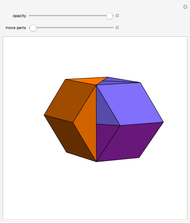
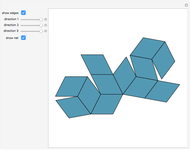
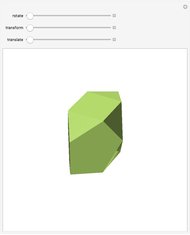
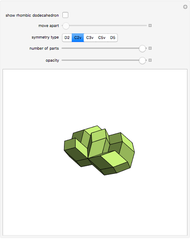
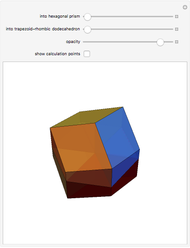
This Demonstration shows the dissection of a cube into four pieces to give a rhombic dodecahedron of the second kind.

Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

The volume of the dodecahedron is 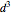/2, where d is the larger diagonal of the golden rhombus. So the edge of the cube has length d/2.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send