Electrostatic Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
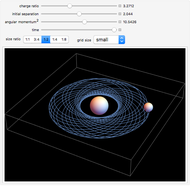
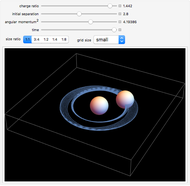
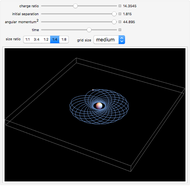
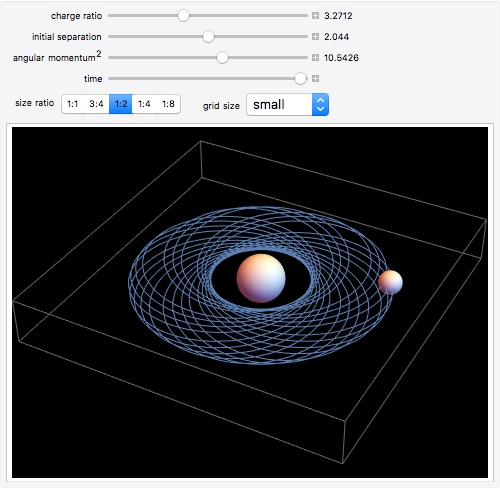
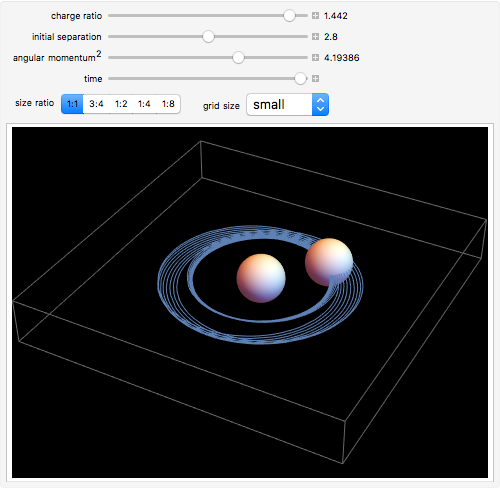
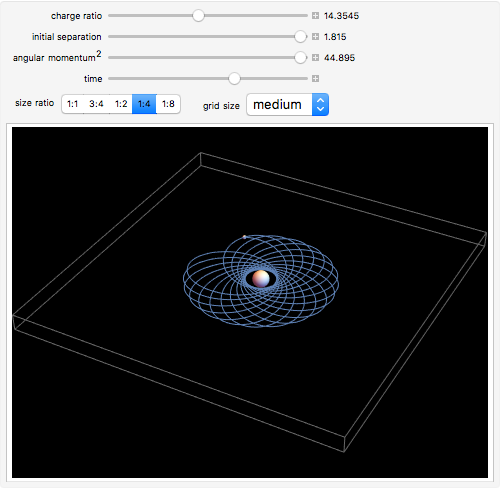
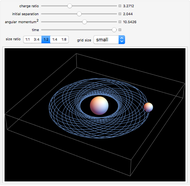
This Demonstration shows the orbit of two charged spheres attracted to each other by electrostatic forces. When the spheres are far apart, the electrostatic force between them can be found using Coulomb's law for point charges. When the spheres are closer to each other, however, the actual force becomes much larger than Coulomb's law predictions. This difference is caused by large polarization of the charge on each sphere (the charge distributions become asymmetric) as their separation becomes relatively small. By adjusting their initial separation, charge ratio, and size ratio and then giving them some angular momentum, it is possible to create and sustain a binary orbiting system. This Demonstration initially sets these factors to create a stable, circular orbit for each size ratio. By increasing or decreasing the other values, the orbits will become "unstable," which can be seen by an early collision, a wobbly orbital pattern, or an escaping orbit with a hyperbolic trajectory.
Contributed by: Stefan McCarty (December 2011)
With additional contributions by: Shubho Banerjee
Open content licensed under CC BY-NC-SA
Snapshots
Details
Electrostatic orbits generally occur in nature only on a microscopic scale (i.e. the electron orbiting the nucleus). This is because larger versions of the orbits require much more electrostatic energy than is usually available. Even so, a macroscopic version of electrostatic orbits is instructive. This Demonstration shows a simulation of electrostatic orbits that complements theory and experiments that are already available in the literature [1, 2, 3].
For this simulation, Newton's second law  ,
, 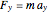 ) is used to numerically solve for the positions of each sphere using Mathematica's built-in function NDSolve. For the electrostatic force between the two spheres, unpublished data [4] is used. The force data was accurately calculated (for several different sphere sizes) at some specific distances using the method of image charges [5]. A fitting function is then used to express the force as a function of the distance. The adjustable parameters that determine the motion of the spheres are the charge ratio of the spheres (with one charge set equal to 1), the size ratio (with one sphere's radius set to 1), the initial center-to-center separation, and the initial angular momentum. One sphere is held fixed, so only the mass of the orbiting sphere is varied. Since the angular momentum is adjustable, the mass of the orbiting sphere can be set equal to 1. The variation of mass is accounted for through the value of the angular momentum [1].
) is used to numerically solve for the positions of each sphere using Mathematica's built-in function NDSolve. For the electrostatic force between the two spheres, unpublished data [4] is used. The force data was accurately calculated (for several different sphere sizes) at some specific distances using the method of image charges [5]. A fitting function is then used to express the force as a function of the distance. The adjustable parameters that determine the motion of the spheres are the charge ratio of the spheres (with one charge set equal to 1), the size ratio (with one sphere's radius set to 1), the initial center-to-center separation, and the initial angular momentum. One sphere is held fixed, so only the mass of the orbiting sphere is varied. Since the angular momentum is adjustable, the mass of the orbiting sphere can be set equal to 1. The variation of mass is accounted for through the value of the angular momentum [1].
References:
[1] S. Banerjee, B. Taylor, and A. Banerjee, "On the Stability of Electrostatic Orbits," American Journal of Physics, 77(5), 2009 pp. 396–400. doi:10.1119/1.3100774.
[2]. S. Banerjee, K. W. Andring, D. L. Campbell, J. A. Janeski, D. A. Keedy, S. P. Quinn, and B. K. Hoffmeister, "Orbital Motion of Electrically Charged Spheres in Microgravity," The Physics Teacher, 46(8), 2008 pp. 460–464. doi:10.1119/1.2999060.
[3] B. K. Hoffmeister, D. A. Meyer, B. M. Atkins, G. A. Franks, J. T. Fuchs, L. Li, C. W. Sliger, and J. E. Thompson, "Orbital Dynamics of Two Electrically Charged Conducting Spheres," America Journal of Physics, 78(10), 2010 pp. 1002–1006. doi:10.1119/1.3456117.
[4] S. Banerjee and E. Nelsen, data to be published.
[5] J. C. Maxwell, A Treatise on Electricity and Magnetism, Vol. 1, New York: Dover, 1954 pp. 281–283.
Permanent Citation
"Electrostatic Orbits"
http://demonstrations.wolfram.com/ElectrostaticOrbits/
Wolfram Demonstrations Project
Published: December 15 2011