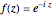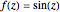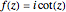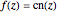Electrostatic Fields Using Conformal Mapping

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A conformal mapping  produces a complex function of a complex variable,
produces a complex function of a complex variable,  , so that the analytical function
, so that the analytical function  maps the complex
maps the complex  plane into the complex
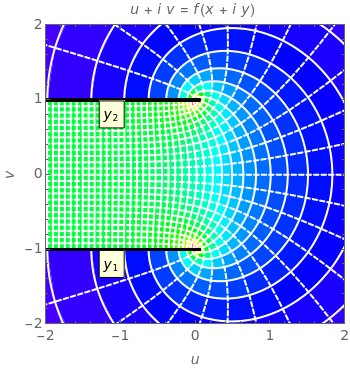
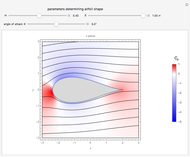
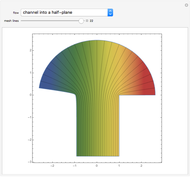
plane into the complex 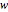 plane. This technique is useful for calculating two-dimensional electric fields: the curve in the
plane. This technique is useful for calculating two-dimensional electric fields: the curve in the 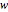 plane where either
plane where either  or
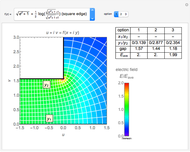
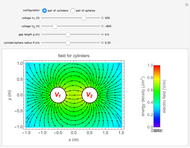
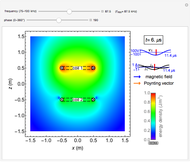
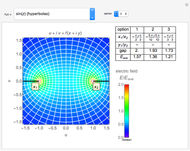
or  is constant corresponds to either an equipotential line or electric flux. This Demonstration shows 10 examples of electrostatic fields often encountered in high voltage applications. The electric field is shown in the
is constant corresponds to either an equipotential line or electric flux. This Demonstration shows 10 examples of electrostatic fields often encountered in high voltage applications. The electric field is shown in the  -
- plane (or the
plane (or the 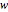 plane, where
plane, where  ). The electrodes correspond to either
). The electrodes correspond to either 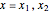 or
or 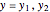 , where
, where  (
( ). The 10 examples are:
). The 10 examples are:
Contributed by: Y. Shibuya (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: field of knife edge to knife edge using 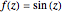
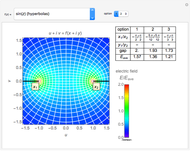
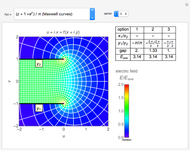
Snapshot 2: field of parallel plate capacitor edge: Maxwell curves using 
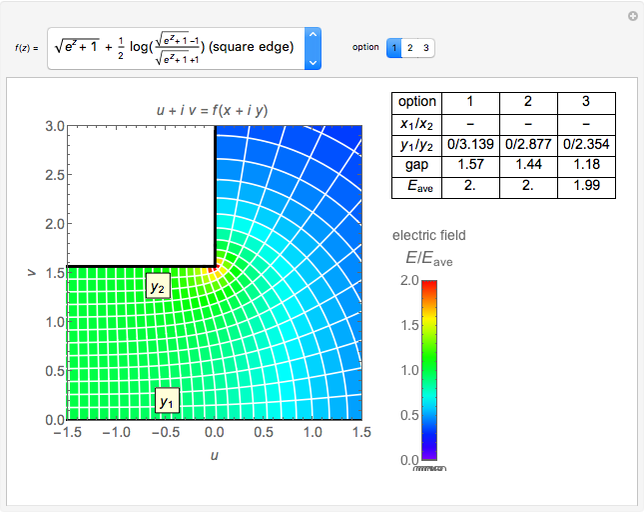
Snapshot 3: field of square edge to plane using a function derived using the Schwarz–Christoffel transformation
When a curve from a constant  represents an equipotential line, the electric field can be calculated from
represents an equipotential line, the electric field can be calculated from  . Therefore, its magnitude is given by
. Therefore, its magnitude is given by
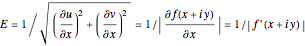 .
.
The calculation is done for a limited number of  and
and  values to save time. Please be patient, particularly for
values to save time. Please be patient, particularly for  and
and  .
.
References
[1] H. Prinz, Hochspannungsfelder, München: R. Oldenbourg Verlag, 1969.
[2] P. Moon and D. E. Spencer, Field Theory Handbook: Including Coordinate Systems, Differential Equations and Their Solutions, 2nd ed., Cleveland: John T. Zubal, 2003.
Permanent Citation