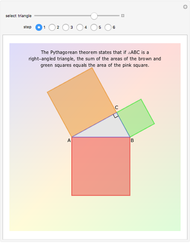
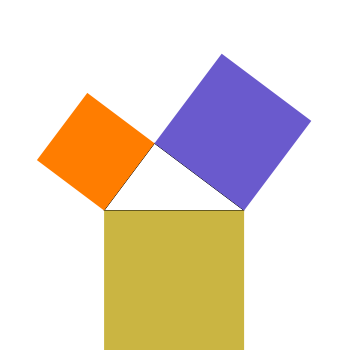Euclid's Proof of the Pythagorean Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
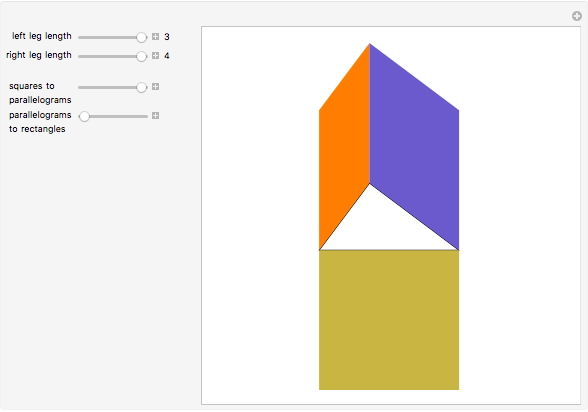
The top two sliders choose lengths of the legs of the right triangle.
[more]
Contributed by: Robert Root (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
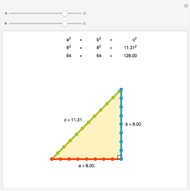
The top two sliders choose lengths of the legs of the right triangle. Side  must have length between 0 and 3, while side
must have length between 0 and 3, while side  has length between 1 and 4, so any ratio of lengths is possible, with the understanding that the short side must be
has length between 1 and 4, so any ratio of lengths is possible, with the understanding that the short side must be  in extreme cases. That is, you can specify a right triangle similar to any right triangle by considering the ratio of the lengths of the legs as the defining characteristic of similarities. The animation works best if both legs are comfortably larger than 0; roughly, the ratio
in extreme cases. That is, you can specify a right triangle similar to any right triangle by considering the ratio of the lengths of the legs as the defining characteristic of similarities. The animation works best if both legs are comfortably larger than 0; roughly, the ratio 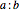 must be nearer unity than 1:10 for the areas to be visible throughout. The default is a 3-4-5 triangle, as shown in the thumbnail view.
must be nearer unity than 1:10 for the areas to be visible throughout. The default is a 3-4-5 triangle, as shown in the thumbnail view.
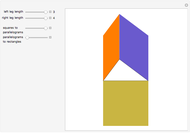
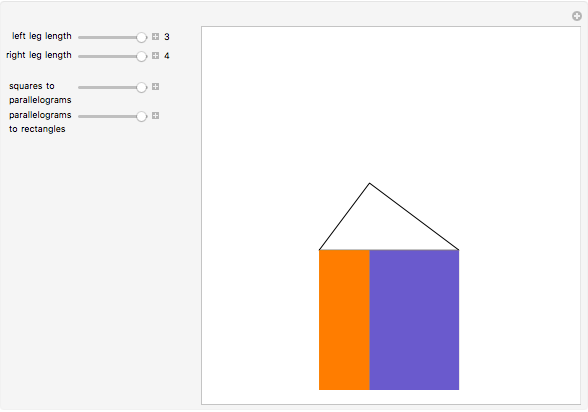
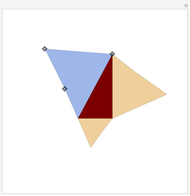
The third slider converts the squares on the legs of the right triangle into parallelograms with equal area and vertical sides. This represents one step in Euclid's proof, demonstrating that the squares shown when the slider control is on the left have the same base and height as the parallelograms shown when the control is in its rightmost position. The top of each parallelogram slides along a line parallel to the leg of the triangle that forms its base until the adjacent sides are vertical, as shown in Snapshot 1. To see this, the last slider needs to be in its leftmost position, but every slider works, no matter the setting of the others.
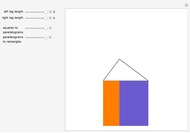
The fourth slider slides the parallelograms down so that they become rectangles occupying the square on the hypotenuse. In Euclid's proof, this represents the Demonstration that the parallelograms, in addition to being equal in area to the squares on the legs, have areas equal to these two rectangles that together can form the square on the hypotenuse, as shown in Snapshot 2. This slider will take the original squares or any intermediate pair of parallelograms to the rectangles with equal area. That is, you can use this slider regardless of the setting of the other three.
Permanent Citation
"Euclid's Proof of the Pythagorean Theorem"
http://demonstrations.wolfram.com/EuclidsProofOfThePythagoreanTheorem/
Wolfram Demonstrations Project
Published: March 7 2011