Another Generalization of Pythagoras's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
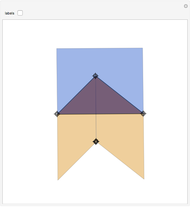
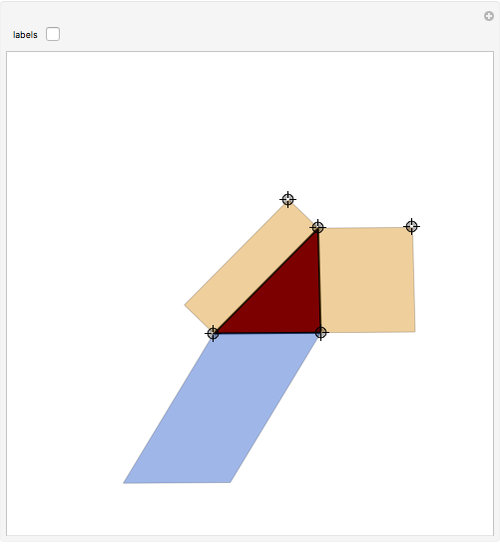
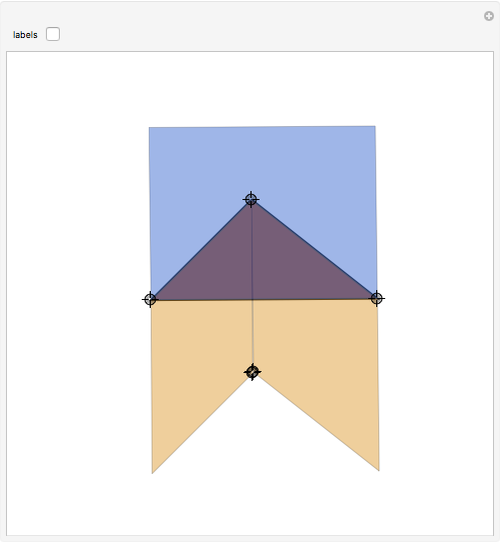
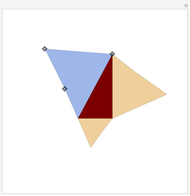
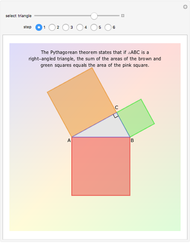
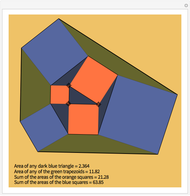
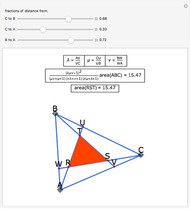
Take any triangle ABC and construct parallelograms ABDE and CBGF that intersect with the triangle only in the sides AB and BC, respectively. Extend ED and FG to meet in H and construct a parallelogram ACKL on the third side AC such that AL and CK are equal and parallel to HB. Then the area of ACKL is the sum of the areas of ABDE and CBGF. In short: the blue area is equal to the sum of the two orange areas.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Another Generalization of Pythagoras's Theorem"
http://demonstrations.wolfram.com/AnotherGeneralizationOfPythagorassTheorem/
Wolfram Demonstrations Project
Published: March 7 2011