Examples of Limits of Real Sequences

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
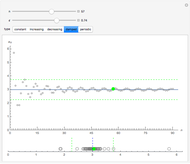
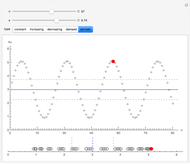
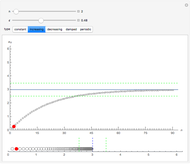
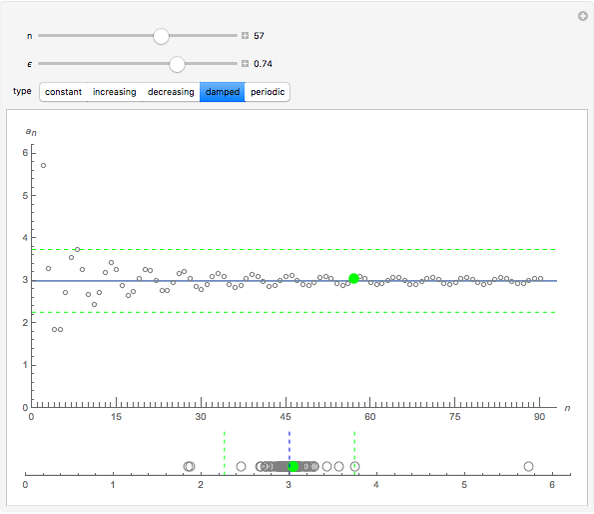
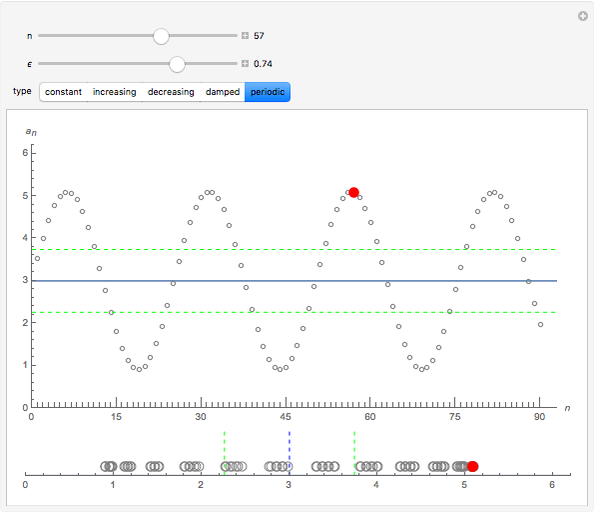
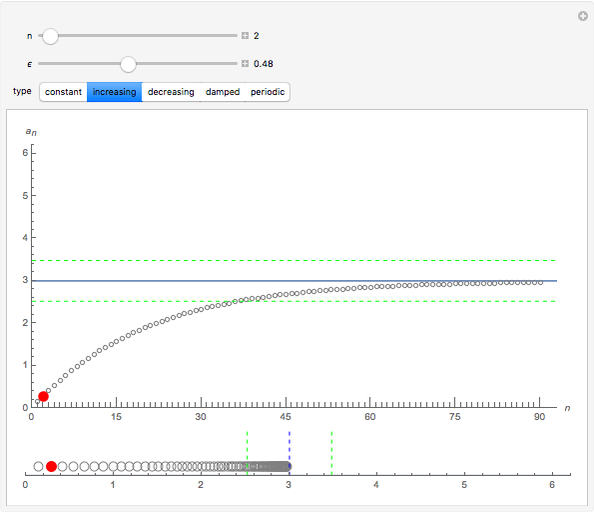
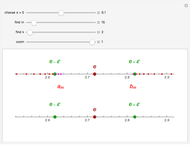
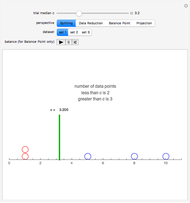
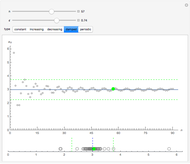
Each of the sequences except for the periodic one appear to converge to 3. The  slider lets you vary the tolerance limit in the definition of the limit. The
slider lets you vary the tolerance limit in the definition of the limit. The  slider lets you plot the
slider lets you plot the 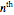 element of the sequence. The color of the point representing the element of the sequence is green within the
element of the sequence. The color of the point representing the element of the sequence is green within the  tolerance region, and red otherwise.
tolerance region, and red otherwise.
Contributed by: Christine Herrera and Alexander White (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration explores the formal definition of the limit of a sequence: a sequence of real numbers 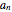 converges to a real number
converges to a real number 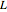 if for every
if for every 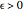 there exists a natural number
there exists a natural number 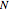 such that
such that 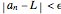 for all
for all 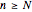 .
.
Use this Demonstration to explore how the different aspects of the formal language of the  -
-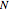 definition relates to the five examples of sequences shown.
definition relates to the five examples of sequences shown.
The concept of limits of sequences is one that students first explore in calculus and later in analysis. Literature has shown that the concept of limits poses potential difficulty for students [2, 4]. In particular, students typically struggle to shift their informal notions of limits to encompass the complexity of the formal definition. Throughout this transition, students draw upon their example space, i.e. the set of examples with which they are familiar [5], and build upon it to make sense of all the different aspects of the formal definition, such as the absolute value inequality, the roles of the universal and existential quantifiers, and the functional relationship between  and
and 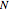 .
.
It is important to note that as students utilize examples to understand the formal definition, there is a potential for cognitive conflict if an example is presented in a visual model that varies from the one that dominates a student’s example space. Students' example spaces may be dominated by either the number line model or the Cartesian plane, and they may have difficulty transitioning between the two different visual models [2]. Thus, to reduce the potential cognitive conflict, the dynamic Mathematica graphs are designed to help students expand their example space to incorporate both models and explore how different examples and their properties relate to the formal definition. Similar dynamic graphs have been shown to help students visualize and understand the formal mathematical language of limits [1, 3].
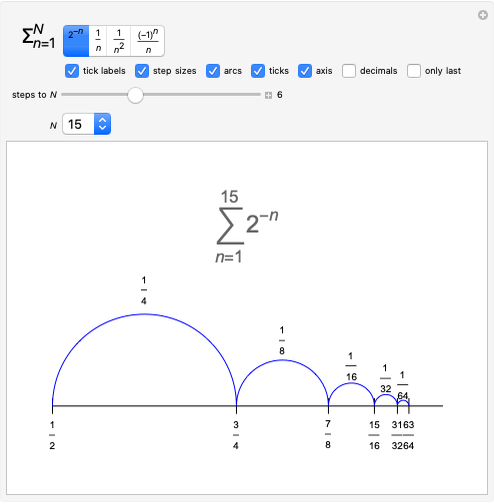
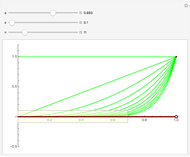
1. Notice the top dynamic model plots the sequence on a Cartesian plane where the horizontal axis is labeled  and the vertical axis
and the vertical axis 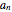 . The same sequence is plotted below on the number line; should it not be labeled
. The same sequence is plotted below on the number line; should it not be labeled  or
or 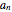 ? Compare the two models: Why is the orientation of the ϵ tolerances different for each of the models? How do they relate?
? Compare the two models: Why is the orientation of the ϵ tolerances different for each of the models? How do they relate?
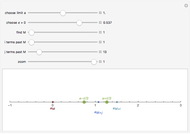
2. Choose the constant sequence. Move the  slider. Move the
slider. Move the  slider. The color of the point representing
slider. The color of the point representing 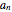 is always green. Why is this true? Relate this to the definition of the limit.
is always green. Why is this true? Relate this to the definition of the limit.
3. Choose the increasing sequence. Move the  slider. Move the
slider. Move the  slider. The color of the point representing
slider. The color of the point representing 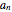 is sometimes green and sometimes red. Why is this true? Relate this to the definition of the limit. Set
is sometimes green and sometimes red. Why is this true? Relate this to the definition of the limit. Set 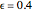 . What is the smallest value of
. What is the smallest value of  for which the point is green—that is, within
for which the point is green—that is, within  of the limit? What is the color for subsequent members of the sequence? What does this tell you about the value of
of the limit? What is the color for subsequent members of the sequence? What does this tell you about the value of 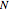 in the limit definition for this choice of
in the limit definition for this choice of  ? If you choose
? If you choose 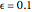 , how does the value
, how does the value 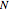 change? Can you find an algebraic form for a sequence
change? Can you find an algebraic form for a sequence 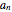 that exhibits this behavior—that is, increasing to a limit of 3?
that exhibits this behavior—that is, increasing to a limit of 3?
4. Choose the decreasing sequence. How is the situation similar to what happens for the increasing sequence? How is it different? Can you modify the algebraic expression you wrote down for the increasing sequence to create a decreasing sequence with a limit of 3?
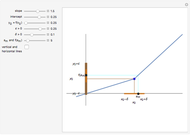
5. Click the damped sequence. Set 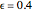 . What is the smallest value of
. What is the smallest value of  for which the point is green—that is, within
for which the point is green—that is, within  of the limit? What is the color for subsequent members of the sequence? Are they all green? For this value of
of the limit? What is the color for subsequent members of the sequence? Are they all green? For this value of  , what is the smallest value of
, what is the smallest value of  for which all the subsequent elements of the sequence are within
for which all the subsequent elements of the sequence are within  of the limit? What does this tell you about the quantifier "for all
of the limit? What does this tell you about the quantifier "for all 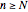 " in the limit definition?
" in the limit definition?
6. Click the periodic sequence. Set 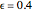 . What is the smallest value of
. What is the smallest value of  for which the point is green—that is, within
for which the point is green—that is, within  of the limit? What is the color for subsequent members of the sequence? Are they all green? For this value of
of the limit? What is the color for subsequent members of the sequence? Are they all green? For this value of  , is there a value of
, is there a value of  for which all the subsequent elements of the sequence are within
for which all the subsequent elements of the sequence are within  of the limit? What does this tell you about the quantifier "for all
of the limit? What does this tell you about the quantifier "for all 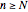 " in the limit definition?
" in the limit definition?
References
[1] B. L. Cory and J. Garofalo, "Using Dynamic Sketches to Enhance Preservice Secondary Mathematics Teachers’ Understanding of Limits of Sequences," Journal for Research in Mathematics Education, 42(1), 2011 pp. 65–97.
[2] C. A. Herrera, "An Investigation of the Relationships between Conceptualization of Limits and Proof Comprehension," PhD dissertation, Texas State University, Texas, 2016.
[3] I. Kidron and N. Zehavi, "The Role of Animation in Teaching the Limit Concept," International Journal of Computer Algebra in Mathematics Education, 9(3), 2002 pp. 205–227.
[4] D. Tall and S. Vinner, "Concept Image and Concept Definition in Mathematics with Particular Reference to Limits and Continuity," Educational Studies in Mathematics, 12(2), 1981 pp. 151–169.
[5] A. Watson and J. Mason, "Extending Example Spaces as a Learning/Teaching Strategy in Mathematics," in PME CONFERENCE 26, 4, 2002 p. 377.
Permanent Citation