Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Successive Differences of Sequences

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

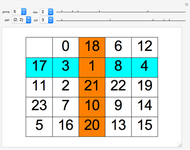
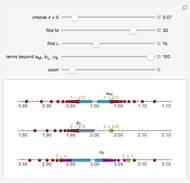
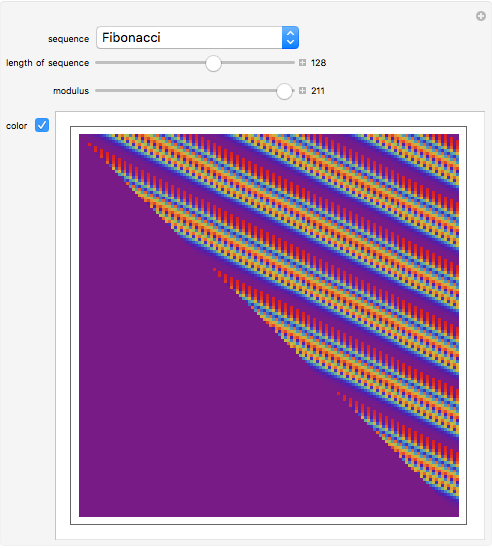
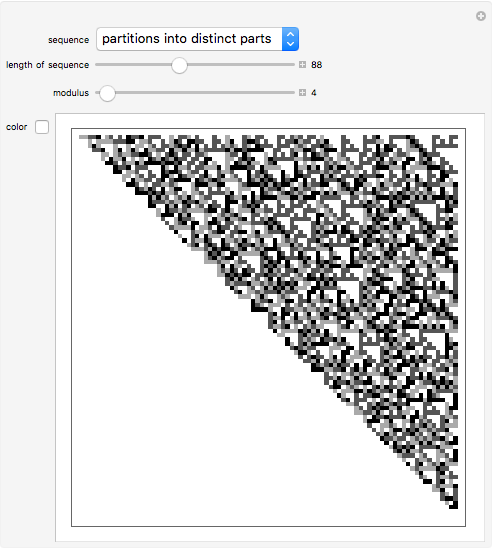
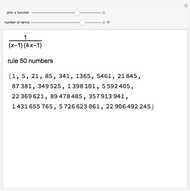
Let be a sequence of numbers . In this Demonstration the sequences are named integer sequences.

[more]

The sequence of differences of is a new sequence .

For example, the sequence of differences of the sequence is . The second differences are the differences of the differences, in this case .

In the graphic, numbers are coded by color. Each row consists of the differences of the row above it, shifted over by one each time. In symbols, the first row is the sequence ; the second row is the sequence ; the third row is ; and so on.

Taking differences is the first thing to try when investigating a sequence.

[less]

Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA

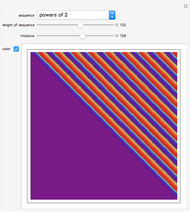
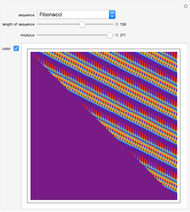
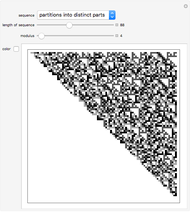
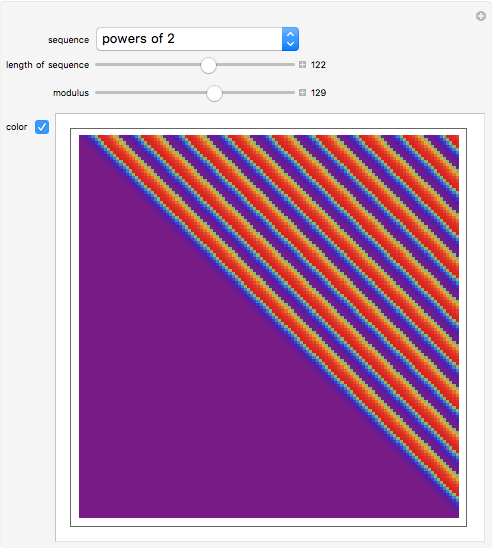
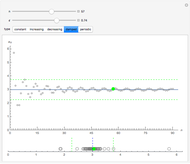
Snapshots

Details

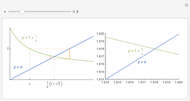
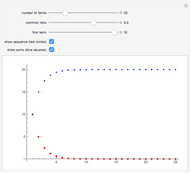
The sequence is often written more compactly as , in analogy with , the infinite sum of the sequence . The notions of sequence and series are related but often mixed up by beginners; sequences are indexed sets of numbers and series add them up. Of course, the sums of integer sequences such as the ones in this Demonstration do not converge in the usual sense.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send