From the Tether Problem to the Involute of a Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
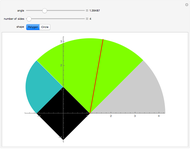
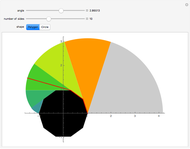
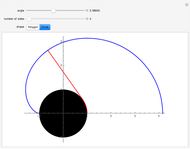
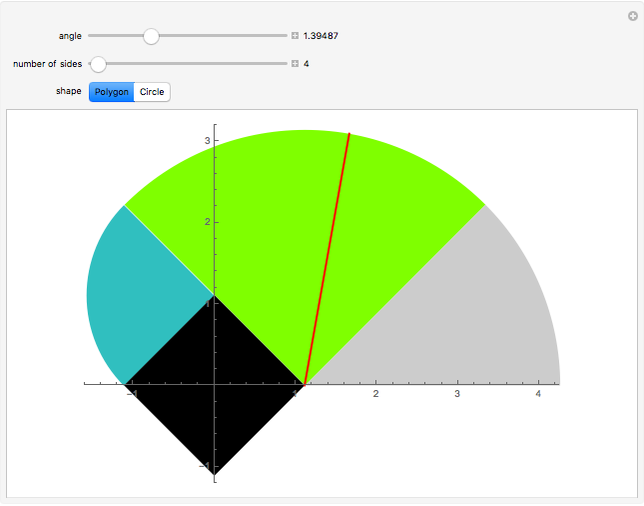
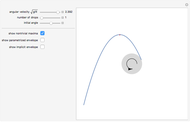
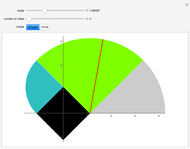
A cow is tethered at the point 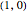 to a black building of semiperimeter
to a black building of semiperimeter 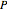 . The figure represents half of the area it can graze with a leash equal to
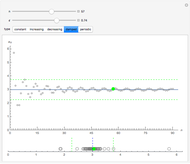
. The figure represents half of the area it can graze with a leash equal to 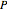 . Change the angle to see what happens as the cow moves around the building. The shape of the base of the building can be either a regular polygon or a circle. If you choose a polygon, use the slider to increase the number of sides.
. Change the angle to see what happens as the cow moves around the building. The shape of the base of the building can be either a regular polygon or a circle. If you choose a polygon, use the slider to increase the number of sides.
Contributed by: Eugene Curtin and Alexander White (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The tether problem is a classic problem from grade school mathematics. A cow is tied to a rectangular building with a leash of fixed length. For given dimensions of the rectangle and length of leash, the student must determine the area of the region the cow is free to graze. The solution involves sectors of circles whose radii depend on where the leash wraps around the corner of the building.
If the building is a silo (i.e. a cylinder), the problem is more difficult. The boundary of the region includes a portion of the involute of a circle, and the area can be determined using multivariate calculus [1]. In this Demonstration (inspired by Archimedes's approximation of  using regular polygons with more and more sides), we show how the elementary approach involving sectors can be extended to the circle case.
using regular polygons with more and more sides), we show how the elementary approach involving sectors can be extended to the circle case.
Suppose the base of the building is a regular  -gon with semiperimeter
-gon with semiperimeter 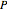 and that the length of the leash is also
and that the length of the leash is also 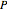 . Focusing on the top half of the polygon and starting opposite to where the leash is tethered, going clockwise, let the vertices be
. Focusing on the top half of the polygon and starting opposite to where the leash is tethered, going clockwise, let the vertices be  , where
, where  . For
. For  , the area
, the area  of the colored sector at
of the colored sector at  depends on the measure of the external angle
depends on the measure of the external angle  and the radius at that vertex
and the radius at that vertex 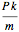 ;
; 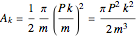 . The sum of the areas of the colored sectors is
. The sum of the areas of the colored sectors is 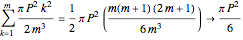 as
as 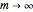 . The area of the gray sector is
. The area of the gray sector is 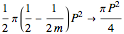 as
as 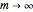 . As
. As 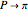 , the area of the sectors converges to
, the area of the sectors converges to  . By symmetry, the total area the cow is free to roam is twice this, or
. By symmetry, the total area the cow is free to roam is twice this, or 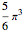 .
.
Reference
[1] D Roy, "The Involute of a Circle," UniversalPhysics.info (blog). (Feb 2, 2012) www.universalphysics.info/the-involute-of-a-circle.
Permanent Citation