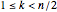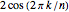Experimenting with Sums of Primitive Roots of Unity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
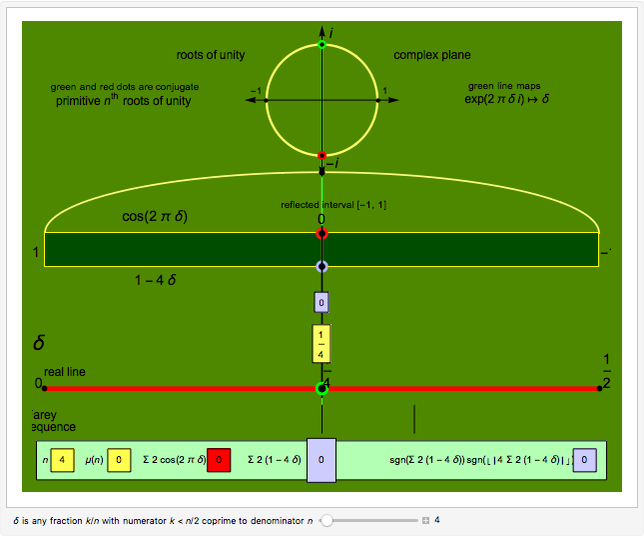
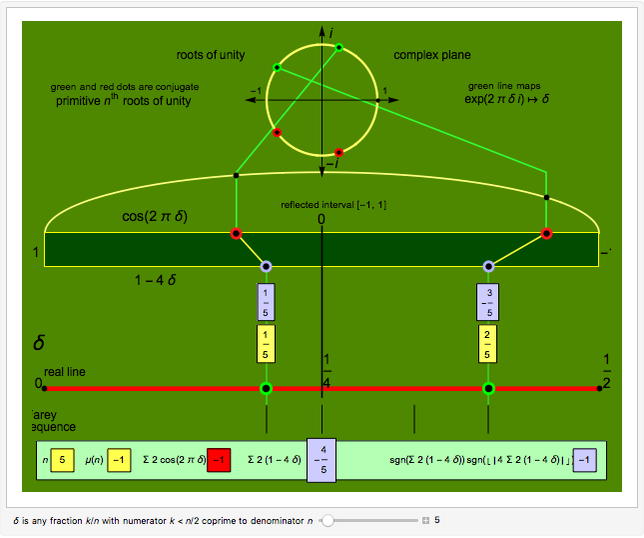
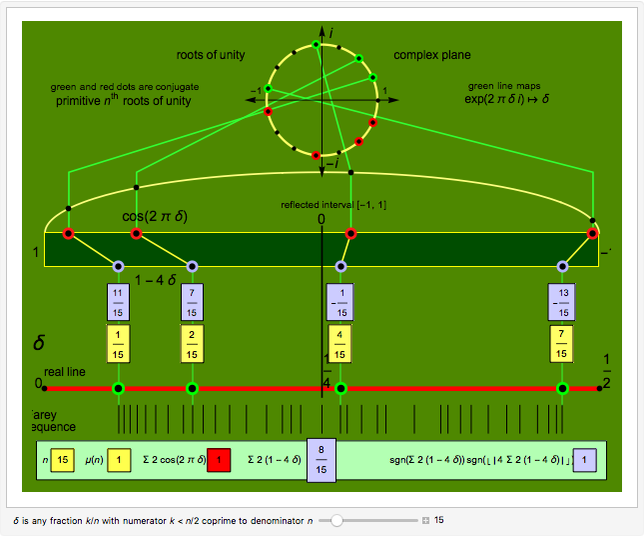
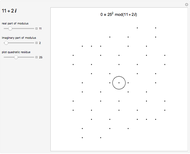
The primitive 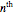 roots of unity are parametrized by the fractions
roots of unity are parametrized by the fractions 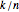 where
where  and
and 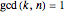 via the complex function
via the complex function 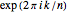 .
.
Contributed by: Jenda Vondra (July 2013)
The author is grateful to Ed Pegg Jr for assistance.
Open content licensed under CC BY-NC-SA
Snapshots
Details
Definitions
The 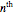 roots of unity are the solutions of the equation
roots of unity are the solutions of the equation  . The
. The  solutions lie equally spaced around the unit circle.
solutions lie equally spaced around the unit circle.
A solution  is called primitive if
is called primitive if 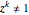 for some
for some  , which occurs when
, which occurs when  is coprime to
is coprime to  [1]. The primitive
[1]. The primitive 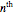 roots of unity are given by
roots of unity are given by 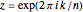 for
for 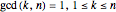 , so there are
, so there are 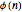 , where
, where  is the Euler totient function [2].
is the Euler totient function [2].
The Möbius function  is defined to be
is defined to be  if
if  is the product of
is the product of  distinct primes, and zero otherwise, with
distinct primes, and zero otherwise, with 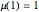 [3].
[3].
Ramanujan's sum  for
for 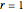 gives
gives 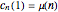 for all positive integers
for all positive integers  [4].
[4].
The Farey sequence of order  is the set of irreducible fractions between 0 and 1 with denominators less than or equal to
is the set of irreducible fractions between 0 and 1 with denominators less than or equal to  , arranged in increasing order [5].
, arranged in increasing order [5].
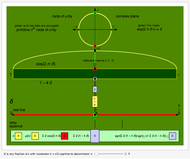
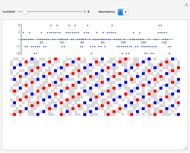
For the purpose of this Demonstration, we omit the fraction 0/1 and truncate the sequence to include only the fractions less than  . The sequence is
. The sequence is 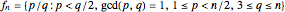 . The truncated Farey sequence is plotted as the black "barcode" and is scaled to the real interval
. The truncated Farey sequence is plotted as the black "barcode" and is scaled to the real interval 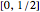 where the fractions
where the fractions  are those Farey fractions with denominator
are those Farey fractions with denominator  and the remaining bars are the Farey fractions with denominators less than
and the remaining bars are the Farey fractions with denominators less than  .
.
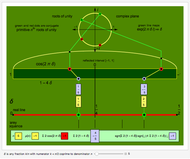
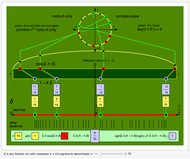
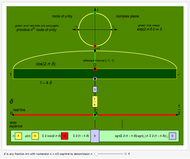
Demonstration
Euler's formula  (for
(for  as before) plots the primitive
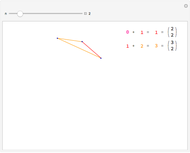
as before) plots the primitive 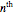 roots of unity on the unit circle in the complex plane. Upon summing, their symmetries allow cancellation of the imaginary parts and duplication of the real parts to give the shortened summation
roots of unity on the unit circle in the complex plane. Upon summing, their symmetries allow cancellation of the imaginary parts and duplication of the real parts to give the shortened summation
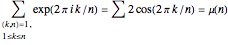 , where
, where  stands
stands 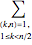 here and in the following.
here and in the following.
In the result, this sum is shown as 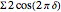 , where
, where  denotes the fraction
denotes the fraction 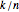 .
.
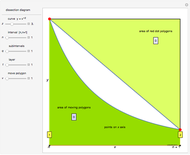
Plotting the points 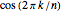 illustrates how this sum is a measure of their asymmetry about the point zero, seemingly miraculously always equal to
illustrates how this sum is a measure of their asymmetry about the point zero, seemingly miraculously always equal to 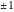 or
or  for any natural number
for any natural number  .
.
The Demonstration then plots the points 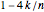 with a visual link to each point
with a visual link to each point 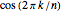 and computes the comparable sum
and computes the comparable sum 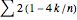 .
.
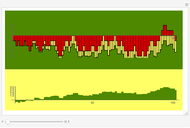
Computations for  up to
up to 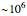 show that the sign of
show that the sign of 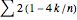 matches the Möbius function for squarefree
matches the Möbius function for squarefree  and the sign of
and the sign of 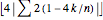 (where
(where 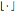 is the floor function) matches the Möbius function for non-squarefree
is the floor function) matches the Möbius function for non-squarefree  and is positive for squarefree
and is positive for squarefree  .
.
The product of the sign functions gives an algorithm that returns the Möbius function value;
 for
for  .
.
Writing 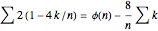 gives the Möbius function in terms of the totient function and the partial sum of the coprime numbers (to
gives the Möbius function in terms of the totient function and the partial sum of the coprime numbers (to  ) that it counts;
) that it counts;
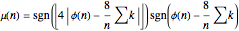 for
for  .
.
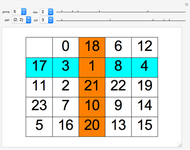
Ranging through selected denominators 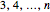 shows the fractions
shows the fractions  that form the truncated Farey sequence
that form the truncated Farey sequence  .
.
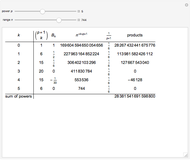
Let 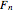 be the Farey sequence of order
be the Farey sequence of order  ; a classical sum [6] of the primitive roots of unity gives
; a classical sum [6] of the primitive roots of unity gives
 , which reduces to
, which reduces to 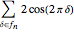 .
.
The analogous sum 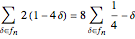 correlates to the classic discrepancy sum
correlates to the classic discrepancy sum 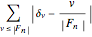 that measures distribution in the Farey sequence
that measures distribution in the Farey sequence 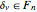 .
.
The sum  measures asymmetry in the distribution of the Farey sequence
measures asymmetry in the distribution of the Farey sequence  about
about  .
.
From the well-known uniform distribution modulo one of the Farey sequence, it follows that  tends to zero as
tends to zero as  tends to infinity.
tends to infinity.
References
[1] Wikipedia. "Root of Unity." (May 8, 2013) en.wikipedia.org/wiki/Root_of_unity.
[2] Wikipedia. "Euler's Totient Function. (Jun 13, 2013) en.wikipedia.org/wiki/Euler%27s_totient_function.
[3] Wikipedia. "Möbius Function." (Jun 17, 2013) en.wikipedia.org/wiki/Mobius_function.
[4] Wikipedia. "Ramanujan's Sum." (Mar 19, 2013) en.wikipedia.org/wiki/Ramanujan%27s_sum.
[5] Wikipedia. "Farey Sequence." (Jun 9, 2013) en.wikipedia.org/wiki/Farey_sequence.
[6] Wikipedia. "Mertens Function." (May 3, 2013) en.wikipedia.org/wiki/Mertens_function.
[7] M. N. Huxley, "The Distribution of Farey Points, I," Acta Arithmetica, 18, 1971 pp. 281–287. matwbn.icm.edu.pl/ksiazki/aa/aa18/aa18130.pdf.
Permanent Citation