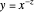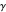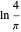Proofs Using a Quadrature Method of Archimedes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
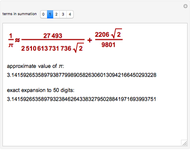
Archimedes divided a segment of a parabola into increasingly many diminishing triangles. Having deduced the area of each triangle and observing that the areas formed a geometric sequence, he found the area by summing the geometric series [1].
[more]
Contributed by: Jenda Vondra (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
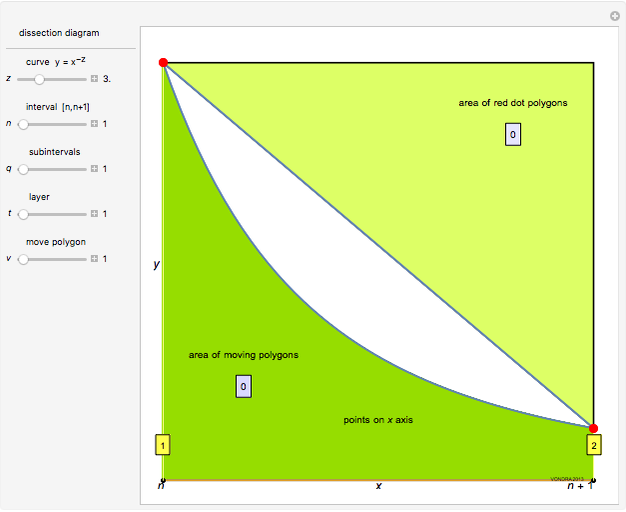
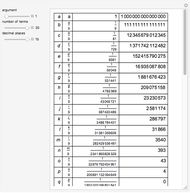
The variables 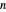 ,
,  ,
,  ,
,  are positive integers and
are positive integers and  is real and non-negative.
is real and non-negative.
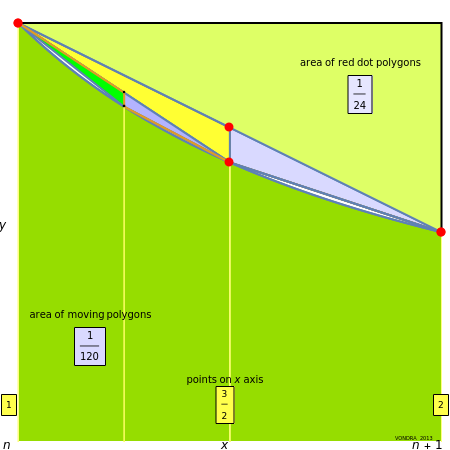
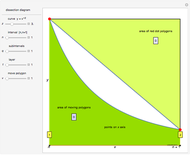
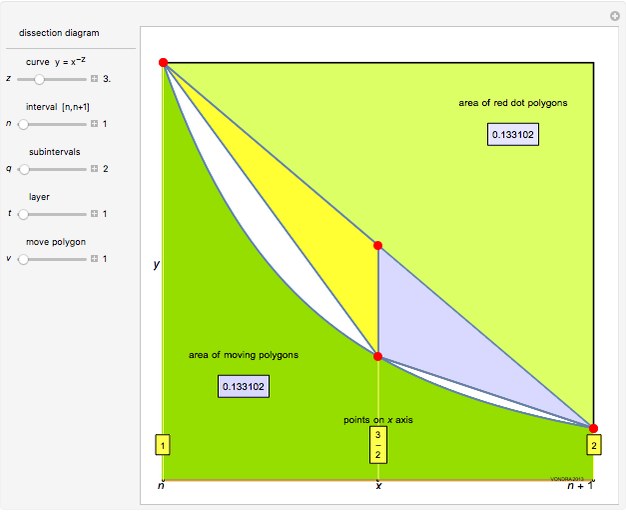
This Demonstration plots the curve 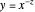 over the interval
over the interval 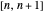 ,
, 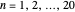 . The vertical lines at
. The vertical lines at  intersect the curve and the line from
intersect the curve and the line from 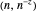 to
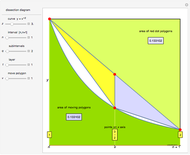
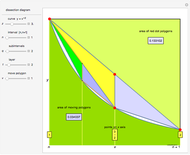
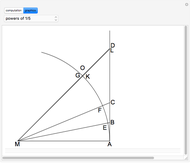
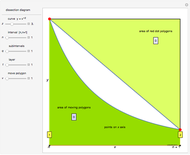
to 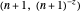 at red points; those points form nonoverlapping polygons. The regions between the curve and the secants joining the red points on the curve can be partially filled by polygons, too; this is the second layer. In general, the area of each polygon formed at layer
at red points; those points form nonoverlapping polygons. The regions between the curve and the secants joining the red points on the curve can be partially filled by polygons, too; this is the second layer. In general, the area of each polygon formed at layer  at position
at position  on the interval
on the interval 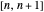 is computed and approximated.
is computed and approximated.
The area 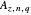 of the polygon with end vertices on the curve at
of the polygon with end vertices on the curve at 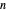 and
and 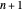 is precisely the sum of the areas of the yellow and the gray triangles with red dots at vertices shown in the diagram, so the expression for the area is
is precisely the sum of the areas of the yellow and the gray triangles with red dots at vertices shown in the diagram, so the expression for the area is
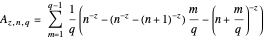 .
.
For example, 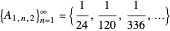 .
.
The limit  as
as 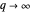 gives the closed area above the curve, and is in principle the method of Riemann integration.
gives the closed area above the curve, and is in principle the method of Riemann integration.
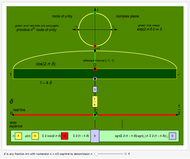
The area 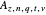 of the polygon with end vertices on the curve at
of the polygon with end vertices on the curve at 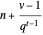 and
and 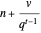 at layer
at layer  at position
at position  on the interval
on the interval 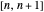 is
is
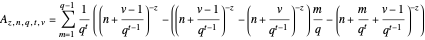 ,
, 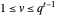 , with value shown in the diagram as "area of moving polygon".
, with value shown in the diagram as "area of moving polygon".
Considering the polygons as a series of "layers" is key to the following algebra.
Re-indexing  as used in the diagram plot rewrites the
as used in the diagram plot rewrites the 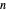
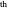 term of the infinite sequence of polygon areas in a layer
term of the infinite sequence of polygon areas in a layer  as
as
 , giving
, giving  .
.
The sum of the first layer of polygon areas on the infinite curve is then 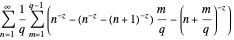 and the sum of all polygon layers is
and the sum of all polygon layers is
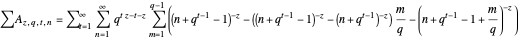 .
.
This can be simplified to
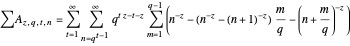 .
.
Rearranging the order of summation into tuples in order of size produces the single sum over  , which is easier to compute:
, which is easier to compute:
 .
.
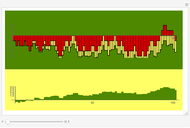
Looking at the dissection diagram and its algebraic expression lets us see many polygon dissections for given closed areas.
Putting 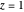 in the diagram plots the hyperbola
in the diagram plots the hyperbola  and we observe a sum of polygon areas giving the identity
and we observe a sum of polygon areas giving the identity
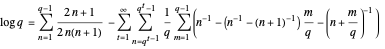
Putting  we observe
we observe
Theorem 1
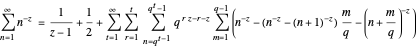 for
for  .
.
Proof
The term 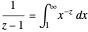 is the area under the curve for
is the area under the curve for 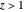 .
.
The term  is the total area of the right triangles above the curve at positive integer points, and by telescoping is constant for
is the total area of the right triangles above the curve at positive integer points, and by telescoping is constant for 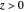 .
.
The term 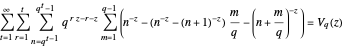 is the total area of all polygons on the infinite curve.
is the total area of all polygons on the infinite curve.
At the special value 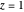 ,
, 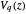 gives the Euler–Mascheroni constant
gives the Euler–Mascheroni constant  (see [2]).
(see [2]).
The sum 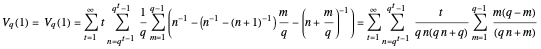 .
.
Rewriting 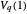 shows the Vacca-type rational series for the Euler–Masceroni constant
shows the Vacca-type rational series for the Euler–Masceroni constant 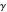 due to Sondow [3, 4].
due to Sondow [3, 4].
 for
for  a positive integer greater than 1 [3].
a positive integer greater than 1 [3].
Putting  , we observe
, we observe
Theorem 2
 for
for 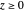 .
.
Proof
The term 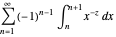 alternates the areas under the curve. Writing the integrals gives the term as
alternates the areas under the curve. Writing the integrals gives the term as
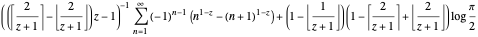 ,
,
with the factor 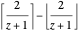 excising the pole in the expression when
excising the pole in the expression when 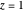 and the term value is
and the term value is  ;
;  and
and 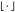 are the ceiling and floor functions, respectively.
are the ceiling and floor functions, respectively.
The term  is the alternating sum of the right triangle areas above the curve at positive integer points.
is the alternating sum of the right triangle areas above the curve at positive integer points.
The term 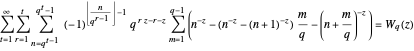 alternates the summation of the areas of all the polygons on the curve.
alternates the summation of the areas of all the polygons on the curve.
At the special value 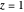 ,
, 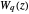 gives the constant
gives the constant 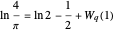 (see [3, 4]);
(see [3, 4]); 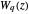 relates to a problem mentioned in [4].
relates to a problem mentioned in [4].
References
[1] Wikipedia. "The Quadrature of the Parabola." (Oct 23, 2013) en.wikipedia.org/wiki/The_Quadrature_of _the _Parabola.
[2] Wikipedia. "Euler–Mascheroni Constant." (Jul 5, 2013) en.wikipedia.org/wiki/Euler-Mascheroni_constant.
[3] J. Sondow, "New Vacca-Type Rational Series for Euler's Constant and Its 'Alternating' Analog 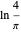 ."arxiv.org/abs/math/0508042v1.
."arxiv.org/abs/math/0508042v1.
[4] J. Sondow, "New Vacca-Type Rational Series for Euler's Constant  and Its 'Alternating' Analog
and Its 'Alternating' Analog 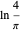 ," Additive Number Theory (D. Chudnovsky, ed.), New York, NY: Springer, 2010 pp. 331–340. link.springer.com/chapter/10.1007%2 F978-0-387-68361-4_ 23.
," Additive Number Theory (D. Chudnovsky, ed.), New York, NY: Springer, 2010 pp. 331–340. link.springer.com/chapter/10.1007%2 F978-0-387-68361-4_ 23.
Permanent Citation