Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Two Enumerations of the Rationals

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

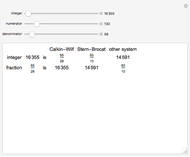
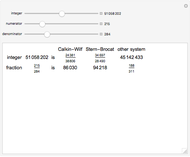
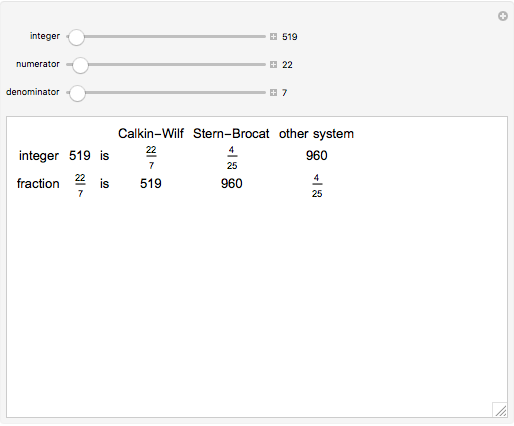
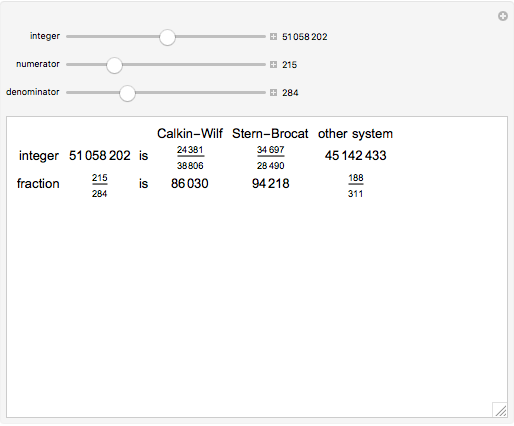
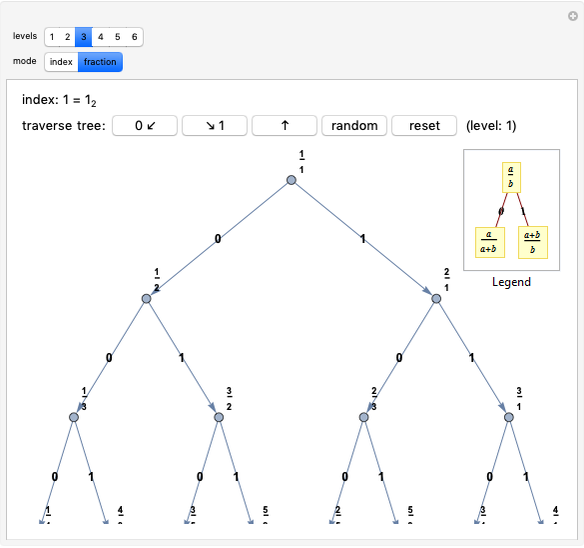
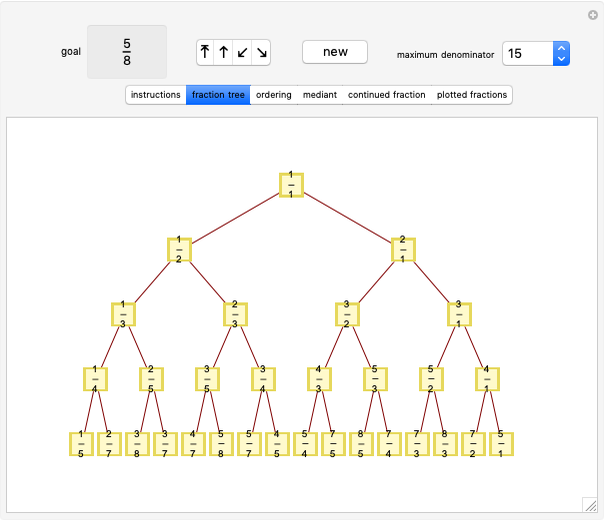
Here are two methods for enumerating the rational numbers. The Calkin–Wilf method starts with corresponding to the binary number 1. If the binary number corresponds to the fraction , then the binary number corresponding to is 0 appended to , and the one corresponding to is 1 appended to . According to this scheme, the Calkin–Wilf enumeration begins with , where semicolons separate the rows of an array.

[more]

The Stern–Brocat method is more complicated, but it winds up reversing the Calkin–Wilf binary number except for the leading 1. The corresponding enumeration then reads .

Since either of the above arrays can be put into one-to-one correspondence with the set of natural numbers (positive integers) ℕ, the rationals must also comprise a set of cardinality .

[less]

Contributed by: Ed Pegg Jr (September 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send