Focus-Directrix Property of an Ellipse with Dandelin Spheres

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
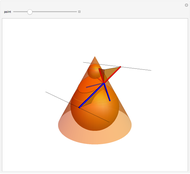
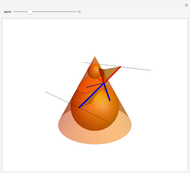
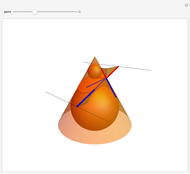
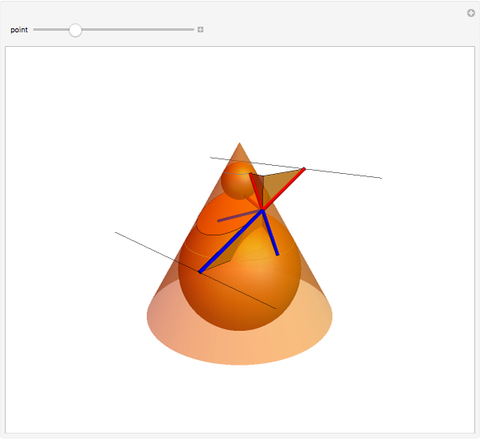
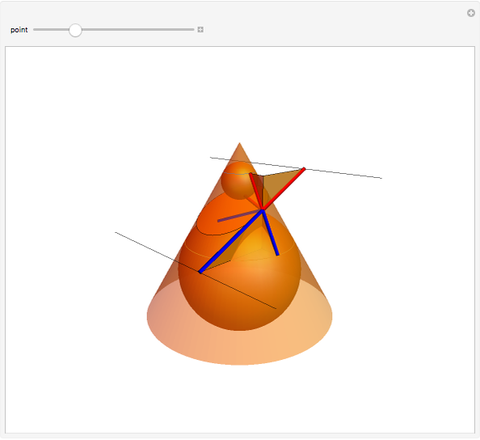
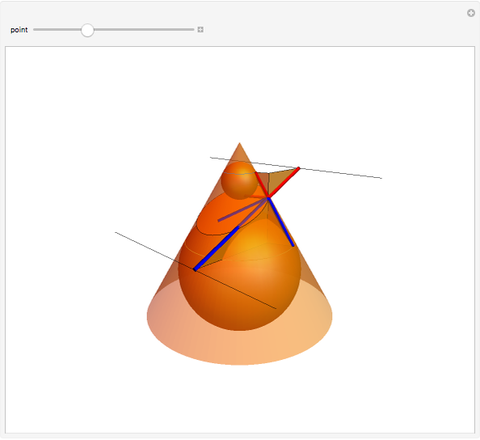
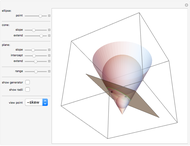
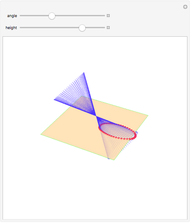
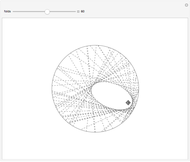
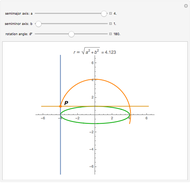
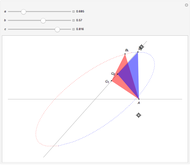
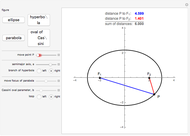
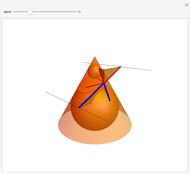
This Demonstration shows a plane cutting a cone in an ellipse; the two spheres tangent to the plane and the cone meet the cone in two circles. The spheres meet the plane at the foci of the ellipse. The directrices are the lines where the cutting plane meets the planes of the circles of contact.
[more]
Contributed by: Khalid Bin Walid (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Focus-Directrix Property of an Ellipse with Dandelin Spheres"
http://demonstrations.wolfram.com/FocusDirectrixPropertyOfAnEllipseWithDandelinSpheres/
Wolfram Demonstrations Project
Published: August 6 2014