Dandelin Spheres for an Ellipse

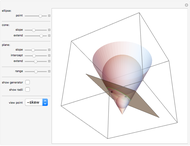
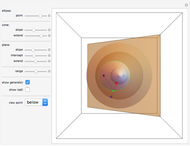
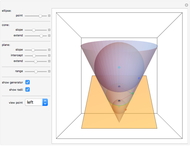
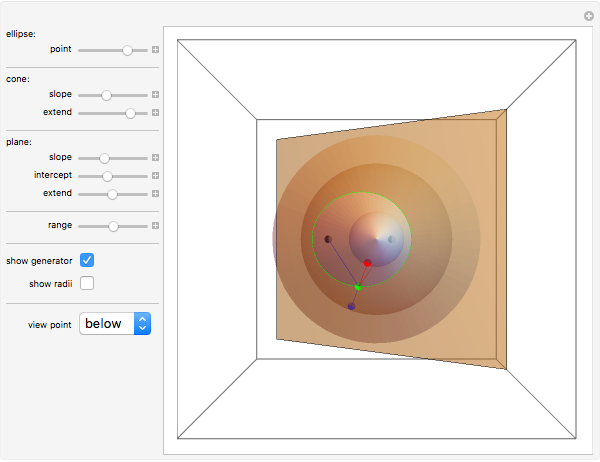
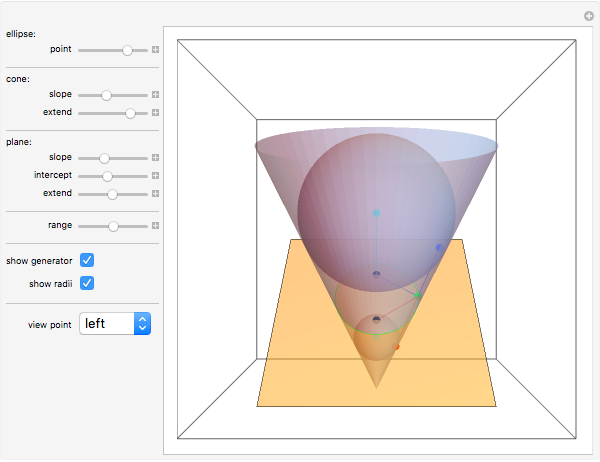
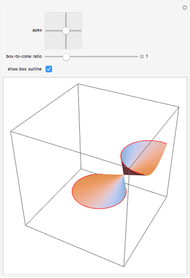
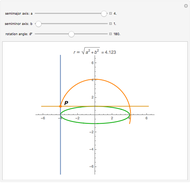
Slice a cone with a plane so that the intersection is bounded. Although it might appear that the section is an oval that is fatter on the more open part of the cone, in fact the section is an ellipse.

To see this, consider the following line of reasoning.

Recall that an ellipse can be defined as the set of points the sum of whose distances from the foci is constant.

Among the spheres tangent to the cone, draw the two (the Dandelin spheres) that are also tangent to the cutting plane, one on each side, and call them and . They touch the cone in two parallel circles. The line segments on a line from the apex (a generator) between the two circles all have the same length.

Drop radii from the centers of the spheres perpendicular to the plane. Those two projected points will turn out to be the foci of the ellipse, and .

Take a point on the curve. Draw lines from to the foci. Because is in the plane, those lines are tangent to the respective spheres.

Draw a generator from the apex of the cone through . Such a line is tangent to the spheres, say at and . Those points lie on the parallel circles mentioned, and so the length is constant. Because and are both tangent to , they are equal in length. Similarly, . Finally, is constant.