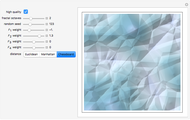
Fractal Cellular Textures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
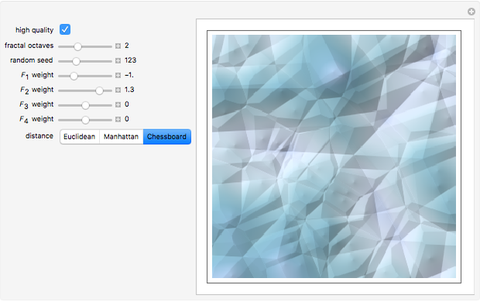
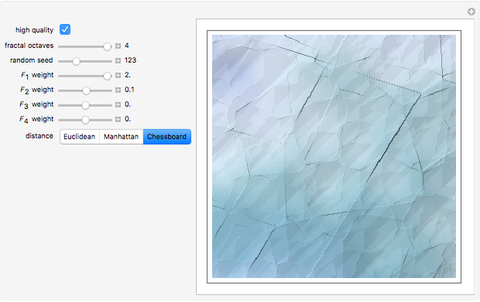
In the synthesis of natural-looking textures, it is common to mimic the self-similarity found in many natural (fractal) systems by mixing copies of a synthetic texture generated at different scales. A "fractal" texture is typically produced by summing the first few "octaves" of a particular texture function. In this case, we use Worley's cellular texture, which combines the first few nearest-neighbor distance functions, 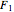 to
to  , for a set of random feature points. Adjust the weights of
, for a set of random feature points. Adjust the weights of 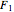 to
to  with the sliders. Interesting results can also be obtained using alternate distance metrics.
with the sliders. Interesting results can also be obtained using alternate distance metrics.
Contributed by: Arnie Cachelin (October 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is based on S. Worley, "A Cellular Texture Basis Function," in SIGGRAPH '96 Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New York: Association for Computing Machinery, 1996 pp. 291–294.
Given a set of random feature points, we can compute the distance from any point 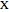 to the nearest feature point. Call this nearest-feature distance function
to the nearest feature point. Call this nearest-feature distance function 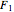 . The function that returns the distance to the second nearest feature is
. The function that returns the distance to the second nearest feature is  , and the
, and the  nearest-feature distance,
nearest-feature distance, 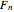 . Cellular textures, Worley observed, can be generated from linear combinations of the first few
. Cellular textures, Worley observed, can be generated from linear combinations of the first few 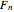 . Producing fractal versions of these texture functions can reproduce interesting natural-looking textures with minimal information input.
. Producing fractal versions of these texture functions can reproduce interesting natural-looking textures with minimal information input.
Permanent Citation