Line Jaggedness Visualization with the Mandelbrot-Weierstrass Function

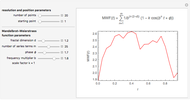
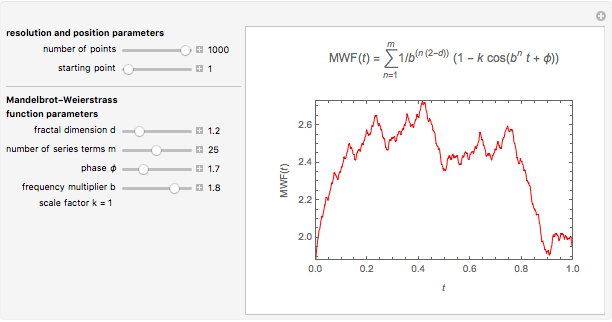
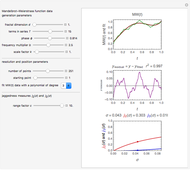
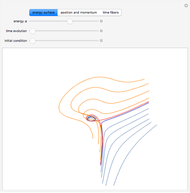
Snapshot 1: moderately jagged line at low resolution

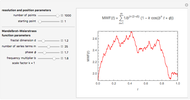
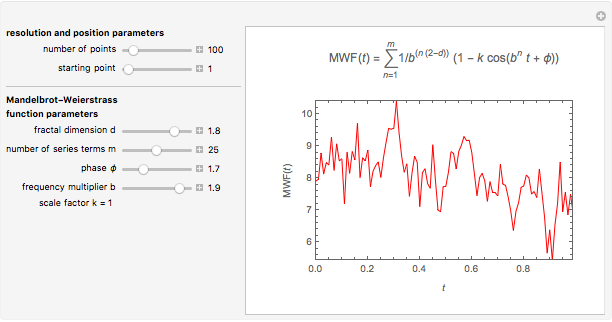
Snapshot 2: moderately jagged line at high resolution

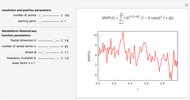
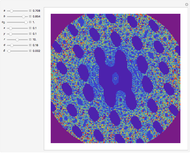
Snapshot 3: highly jagged line at low resolution

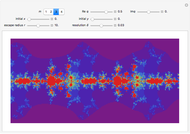
Snapshot 4: highly jagged line at high resolution

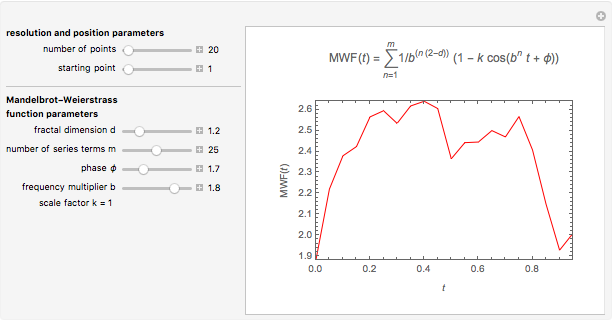
This Demonstration helps the user to visualize the jaggedness of an irregular line, time series, or signature by allowing its generation at different apparent fractal dimensions (in the range 1 to 2) using the Mandelbrot–Weierstrass function as the model. The function is displayed above the plot. The values of four of the function's five parameters , , 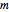, and are set using sliders while is fixed at 1; is the apparent fractal dimension, 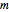is the number of terms computed from the infinite series, is the phase, is the frequency multiplier, and is the scale factor. The number of generated points, which determines the resolution and the starting point in the plot, is also entered with sliders. You can create plots of controlled jaggedness and resolution whose morphology is different in detail. This highlights the roles of the mathematical jaggedness as represented by the fractal dimension and the resolution that in real plots is determined by practical considerations.

References:

R. S. Pande, A. Jalgaonkar, and R. M. Patrikar, "A 3-D FEM Based Extractor for MEMS Inductor with Monte-Carlo Sampling," in Physics of Semiconductor Devices, IEEE Explore, 2007 pp. 710–713.

J. C. Russ, Fractal Surfaces, New York: Plenum Press, 1994 pp. 27–57.

M. Peleg, "Line Jaggedness Measures and Their Applications in Textural Evaluation of Foods," Critical Reviews in Food Science and Nutrition, 37, 1997 pp. 491–518.