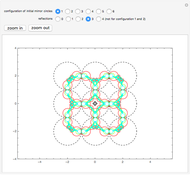
Fractals Generated by Multiple Reflections of Circles
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
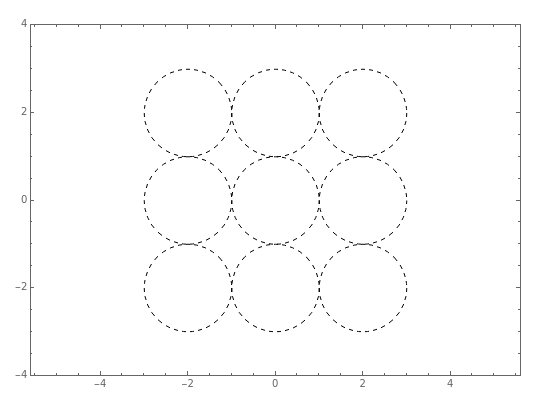
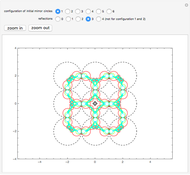
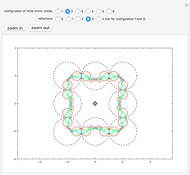
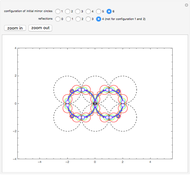
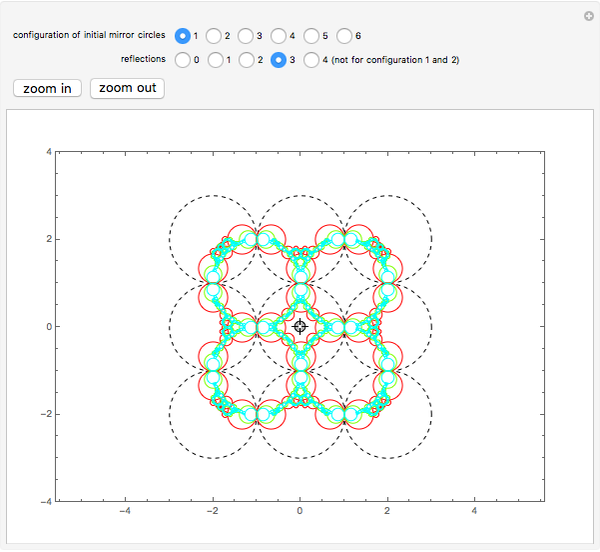
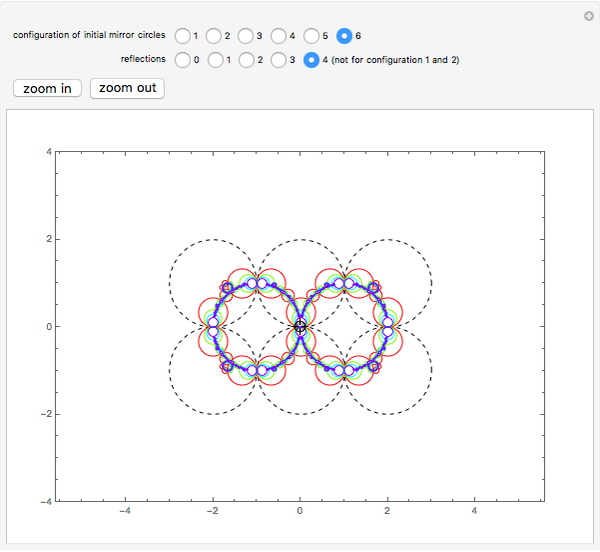
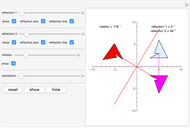
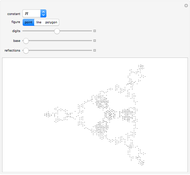
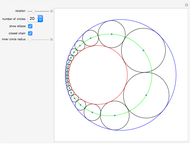
The original circles reflect each other a certain number of times to form a larger configuration of circles.
Contributed by: Yuncong Ma (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
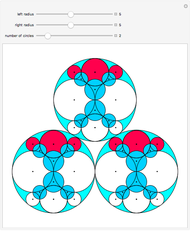
The self-conformal iterated function system comes from the mapping involving circular arcs that are tangent to their neighboring circle arcs.
Permanent Citation
"Fractals Generated by Multiple Reflections of Circles"
http://demonstrations.wolfram.com/FractalsGeneratedByMultipleReflectionsOfCircles/
Wolfram Demonstrations Project
Published: March 7 2011
Fractal Reflection of Circle Configurations
Yuncong Ma
The Completion of Pappus' Chain of Circles
Abraham Gadalla
Dual Billiards
George Beck
Circle Reflections
Michael Trott
Multiple Reflections of a Rotating Triangle
George Beck
Generating a Lemniscate I: Envelope of Circles
Jaime Rangel-Mondragon
Rotation as Product of Two Reflections
Ted Frazier
Selected Reflections in the Sides of a Regular Polygon
Michael Trott
Steiner Chain of Circles
Gregory Hartman
Understanding 2D Reflection
Roger Germundsson
-
Projection of Polytopes into Three Dimensions
Yuncong Ma -
Magnetic Resonance Imaging (MRI)
Yuncong Ma -
Stress-Strain Analysis by the Finite Element Method
Yuncong Ma -
Magic Cube
Yuncong Ma -
Fractals Generated by Multiple Reflections of Circles
Yuncong Ma -
Fractal Reflection of Circle Configurations
Yuncong Ma